题目内容
9.如图1,一次函数y=kx+b的图象交x轴、y轴分别于B、A两点,反比例函数y=$\frac{k}{x}(x<0)$的图象过线段AB的中点C(-2,$\frac{3}{2}$).(1)求反比例函数和一次函数的表达式;
(2)如图2,在反比例函数上存在异于C点的一动点M,过点M作MN⊥x轴于N,在y轴上存在点P,使得S△ACP=2S△MNO,请你求出点P的坐标.
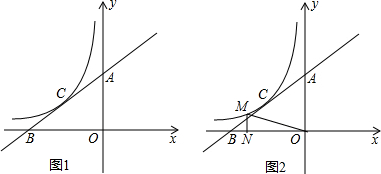
分析 (1)可先根据待定系数法求得反比例函数解析式,然后根据平行线分线段成比例定理求得OA的值,得出A的坐标,把A,C两点分别代入y=kx+b根据待定系数法即可求得.
(2)设P(0,y),则AP=|y-3|.根据反比例函数系数k的几何意义和已知条件求得S△ACP=3,然后根据三角形面积公式得到关于y的方程,解方程即可求得y的值.
解答 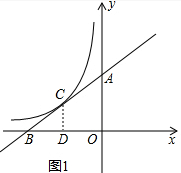 解:(1)如图1,∵反比例函数y=$\frac{k}{x}(x<0)$的图象过点C(-2,$\frac{3}{2}$),
解:(1)如图1,∵反比例函数y=$\frac{k}{x}(x<0)$的图象过点C(-2,$\frac{3}{2}$),
∴k=(-2)×$\frac{3}{2}$=-3,
∴反比例函数解析式为y=-$\frac{3}{x}$;
过点C作CD⊥OB,则CD=$\frac{3}{2}$.
∵CD∥AO,
∴$\frac{BC}{BA}$=$\frac{CD}{AO}$,
即$\frac{1}{2}$=$\frac{\frac{3}{2}}{OA}$,解得:OA=3,
∴A(0,3).
∵一次函数y=kx+b的图象过点C(-2,$\frac{3}{2}$),A(0,3),
∴$\left\{\begin{array}{l}{-2k+b=\frac{3}{2}}\\{b=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$.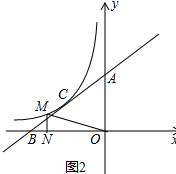
∴一次函数的表达式为y=$\frac{3}{4}$x+3.
(2)如图2,设P(0,y),AP=|y-3|.
∵S△MNO=$\frac{1}{2}$|k|=$\frac{1}{2}$×3=$\frac{3}{2}$,
∴S△ACP=2S△MNO=2×$\frac{3}{2}$=3,
∴$\frac{1}{2}$×AP×|xc|=3,即:$\frac{1}{2}$×|y-3|×2=3;
解得:y=6或y=0.
∴P(0,6)或P(0,0).
点评 本题考查了待定系数法求函数的解析式,平行线分线段成比例定理,三角形的面积等,求得A的坐标是解题的关键.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案| 购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1062 |
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
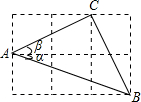 如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)
如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)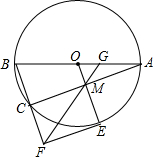 如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M.
如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M.