题目内容
11. 已知二次函数y=-x2+2x+m
已知二次函数y=-x2+2x+m(1)如果二次函数的图象与x轴有两个交点,求m的取值范围.
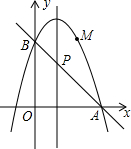
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标;
(3)在第(2)问的条件下,动点M在直线AB上方的抛物线上运动(不与A、B重合),设点M到直线AB的距离为d,求d的最大值.
分析 (1)由抛物线与x轴有两个交点可知△>0,从而得到关于m的不等式,然后求得不等式的解集即可;
(2)将点A的坐标代入抛物线的解析式可求得m的值,从而得到抛物线的解析式,然后将x=0代入抛物线的解析式可求得点B的坐标,然后依据待定系数法可求得直线AB的解析式,然后再求得抛物线的对称轴方程为x=1,最后将x=1代入直线AB的解析式即可求得点P的纵坐标,从而得到点P的坐标;
(3)连接MB、MA、OM,过点M作MD⊥AB,垂足为D,设动点M的坐标为(a,-a2+2a+3),由S△ABM=S△OAM+S△OBM-S△OAB列出△ABM的面积与a的函数关系式,接下来依据配方法可求得△ABM的最大值,最后依据三角形的面积公式可求得DM的长,从而得到d的最大值.
解答 解:(1)∵二次函数的图象与x轴有两个交点,
∴△=22+4m>0.
解得:m>-1.
(2)∵二次函数的图象过点A(3,0),
∴0=-9+6+m.
解得:m=3,
∴二次函数的解析式为:y=-x2+2x+3.
∴抛物线的对称轴为x=1.
∵令x=0,得y=3,
∴B(0,3).
设直线AB的解析式为:y=kx+b.
∵将点A(3,0),(0,3)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,解得:k=-1,b=3,
∴直线AB的解析式为:y=-x+3,
∵把x=1代入y=-x+3得y=2,
∴P(1,2).
(2)如图所示:连接MB、MA、OM,过点M作MD⊥AB,垂足为D.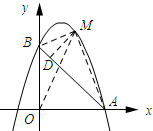
设动点M的坐标为(a,-a2+2a+3).
∵S△ABM=S△OAM+S△OBM-S△OAB=$\frac{1}{2}$×3a+$\frac{1}{2}$×3×(-a2+2a+3)-$\frac{1}{2}$×3×3=$-\frac{3}{2}$a2+$\frac{9}{2}$a=-$\frac{3}{2}$(a-$\frac{3}{2}$)2+$\frac{27}{8}$,
∴当a=$\frac{3}{2}$时,△ABM的面积最大,最大值为$\frac{27}{8}$.
∵OB=0A=3,
∴AB=3$\sqrt{2}$.
∵S△ABM=$\frac{1}{2}$AB•DM,
∴$\frac{1}{2}$×$3\sqrt{2}$•DM=$\frac{27}{8}$.
解得:DM=$\frac{9\sqrt{2}}{8}$.
∴d的最大值为$\frac{9\sqrt{2}}{8}$.
点评 本题主要考查的是二次函数的综合应用,解答本题应用了一元二次方程根的判别式、待定系数法求一次函数的解析式、三角形的面积公式、配方法求二次函数的最值,列出△ABM的面积与点M的横坐标a之间的函数关系式是解题的关键.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案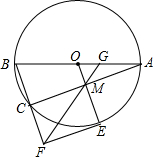 如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M.
如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M. 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=110°,则∠BCD的度数为125°.
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=110°,则∠BCD的度数为125°. 如图,在?ABCD中,AE=CF,M、N分别是BE、DF 的中点,试说明四边形MFNE是平行四边形.
如图,在?ABCD中,AE=CF,M、N分别是BE、DF 的中点,试说明四边形MFNE是平行四边形.