题目内容
17. 如图,在?ABCD中,点E在BC上,AE交BD于点F,如果$\frac{BE}{CE}$=$\frac{3}{2}$,那么$\frac{BF}{DF}$=$\frac{3}{5}$.
如图,在?ABCD中,点E在BC上,AE交BD于点F,如果$\frac{BE}{CE}$=$\frac{3}{2}$,那么$\frac{BF}{DF}$=$\frac{3}{5}$.
分析 由在?ABCD中,且BE:EC=3:2,易得BE:AD=3:5,△ADF∽△EBF,然后根据相似三角形的对应边成比例,即可求得答案.
解答 解:∵BE:EC=3:2,
∴BE:BC=3:5,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴BE:AD=3:5,△ADF∽△EBF,
∴$\frac{BF}{DF}=\frac{BE}{AD}=\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 此题考查了平行四边形的性质,相似三角形的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.在2016年3月12日植树节到来之际,某学校教师分为四个植树小组参加了“大美南阳”的植树节活动,其中三个小组植树的棵数分别为:8,10,12,另一个小组的植树棵数与它们中的一组相同,且这四个数据的众数与平均数相等,则这四个数据的中位数是( )
| A. | 8 | B. | 10 | C. | 12 | D. | 10或12 |
7. 如图,在平行四边形ABCD中,AC、BD相交于点O,则下列结论不一定成立的是( )
如图,在平行四边形ABCD中,AC、BD相交于点O,则下列结论不一定成立的是( )
 如图,在平行四边形ABCD中,AC、BD相交于点O,则下列结论不一定成立的是( )
如图,在平行四边形ABCD中,AC、BD相交于点O,则下列结论不一定成立的是( )| A. | BO=DO | B. | S△COD=S△AOD | C. | ∠BAD=∠BCD | D. | AC=BD |
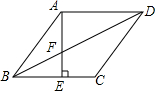 菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论: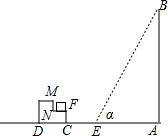 如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.
如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.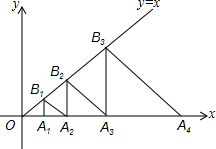 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2016的长为22014.
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1、A2、…、An在x轴上,点B1、B2、…、Bn在直线y=x上,已知OA2=1,则OA2016的长为22014.