题目内容
7.若|a+b+3|+(ab-2)2=0,则a+b=-3,ab=2,a2+b2=5,(a-b)2=1.分析 根据非负数的性质列式求解即可得到a+b和ab的值,再把(a+b)平方,然后根据完全平方公式展开并整理即可求出a2+b2,最后根据完全平方公式整理求解.
解答 解:∵|a+b+3|+(ab-2)2=0,
∴|a+b+3|=0,(ab-2)2=0,
∴a+b+3=0,ab-2=0,
解得a+b=-3,ab=2;
(a+b)2=a2+2ab+b2=9,
∵ab=2,
∴a2+b2=9-2×2=5,
(a-b)2=a2-2ab+b2=5-2×2=1.
故答案为:-3,2;5;1.
点评 本题考查了完全平方公式,非负数的性质,熟练掌握完全平方公式的几个变形式子是解题的关键.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
15.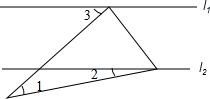 如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
 如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
2.下列几何体中,主视图和俯视图都为矩形的是( )
| A. |  | B. | 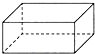 | C. |  | D. | 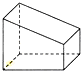 |
12.下列四个数中,最大的数是( )
| A. | |-3| | B. | 30 | C. | 3-1 | D. | $\sqrt{3}$ |
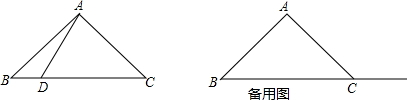
 如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.
如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1. 如图,在?ABCD中,点E在BC上,AE交BD于点F,如果$\frac{BE}{CE}$=$\frac{3}{2}$,那么$\frac{BF}{DF}$=$\frac{3}{5}$.
如图,在?ABCD中,点E在BC上,AE交BD于点F,如果$\frac{BE}{CE}$=$\frac{3}{2}$,那么$\frac{BF}{DF}$=$\frac{3}{5}$.