题目内容
5.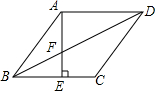 菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:(1)BF为∠ABE的角平分线;
(2)DF=2BF;
(3)2AB2=DF•DB;
(4)sin∠BAE=$\frac{EF}{AF}$.
其中正确的结论为(1)(3)(4)(填序号)
分析 (1)正确.根据菱形性质即可判定.
(2)错误.假设成立推出矛盾即可.
(3)正确.由△ADO∽△FDA,得$\frac{AD}{DF}$=$\frac{DO}{AD}$,AD2=DO•DF,两边乘2即可得到证明
(4)正确.由AD∥BC,得$\frac{EF}{AF}$=$\frac{BE}{AD}$=$\frac{BE}{AB}$,又sin∠BAE=$\frac{EB}{AB}$,由此即可证明.
解答 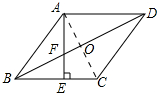
 解:连接AC交BD于点O,
解:连接AC交BD于点O,
∵四边形ABCD是菱形,
∴BD平分∠ABC,BD⊥AC,DO=OB,故(1)正确,
∵AD∥BC,AE⊥BC,
∴AD⊥AE,
∵∠ADO=∠ADF,∠AOD=∠DAF=90°,
∴△ADO∽△FDA,
∴$\frac{AD}{DF}$=$\frac{DO}{AD}$,
∴AD2=DO•DF,
∴2AD2=2DO•DF,
∵AB=AD,BD=2DO,
∴2AB2=DF•DB,故(3)正确,
∵AD∥BC,
∴$\frac{EF}{AF}$=$\frac{BE}{AD}$=$\frac{BE}{AB}$,
∵sin∠BAE=$\frac{EB}{AB}$,
∴sin∠BAE=$\frac{EF}{AF}$,故(4)正确.
∵$\frac{DF}{BF}$=$\frac{AD}{BE}$,
如果DF=2BF,那么AD=2BE,所以BE=EC,这个显然不可能,故②错误,
∴正确的有(1)(3)(4)
故答案为(1)(3)(4).
点评 本题考查菱形的性质、相似三角形的判定和性质、三角函数等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.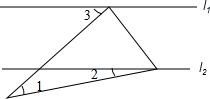 如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
 如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
20. 如图所示,几何体的主视图是( )
如图所示,几何体的主视图是( )
 如图所示,几何体的主视图是( )
如图所示,几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
14.下列方程中,是二元一次方程的是( )
| A. | xy-1=0 | B. | x2+y=3 | C. | $\frac{x}{4}$=3y-1 | D. | x-$\frac{1}{y}$=2 |
15. 下面几何体的主视图是( )
下面几何体的主视图是( )
 下面几何体的主视图是( )
下面几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.
如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.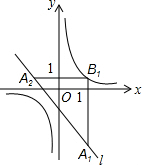 如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1.
如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1. 如图,在?ABCD中,点E在BC上,AE交BD于点F,如果$\frac{BE}{CE}$=$\frac{3}{2}$,那么$\frac{BF}{DF}$=$\frac{3}{5}$.
如图,在?ABCD中,点E在BC上,AE交BD于点F,如果$\frac{BE}{CE}$=$\frac{3}{2}$,那么$\frac{BF}{DF}$=$\frac{3}{5}$.