题目内容
17.利用不等式的性质把下列不等式化成“x>a”或“x<a”的形式.(1)-3x+1>2;
(2)3x>12x;
(3)3x+1>4x+2;
(4)$\frac{1}{3}$x+1>$\frac{1}{2}$x+2.
分析 (1)直接利用不等式的性质化简求出答案;
(2)直接利用不等式的性质化简求出答案;
(3)直接利用不等式的性质化简求出答案;
(4)直接利用不等式的性质化简求出答案.
解答 解:(1)-3x+1>2
-3x>1,
解得:x<-$\frac{1}{3}$;
(2)3x>12x
3x-12x>0,
解得:x<0;
(3)3x+1>4x+2
3x-4x>1,
则-x>1,
解得:x<-1;
(4)$\frac{1}{3}$x+1>$\frac{1}{2}$x+2
$\frac{1}{3}$x-$\frac{1}{2}$x>1,
则-$\frac{1}{6}$x>1,
解得:x<-6.
点评 此题主要考查了不等式的解法,正确解不等式是解题关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
8. 如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
 如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )| A. | 70° | B. | 40° | C. | 35° | D. | 30° |
14.已知⊙O的半径为4cm,直线l与⊙O相切,则圆心O与直线l的距离为( )
| A. | 2cm | B. | 4cm | C. | 8cm | D. | 无法确定 |
 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.当BD=6时,△ABD与△DCE全等.
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.当BD=6时,△ABD与△DCE全等.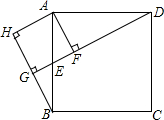 如图,在正方形ABCD中,点E是边AB的中点,过点A作DE的垂线,垂足为F,过点B作DE的垂线,垂足为G,过点A作BG的垂线,垂足为H.求证:四边形AFGH是正方形.
如图,在正方形ABCD中,点E是边AB的中点,过点A作DE的垂线,垂足为F,过点B作DE的垂线,垂足为G,过点A作BG的垂线,垂足为H.求证:四边形AFGH是正方形.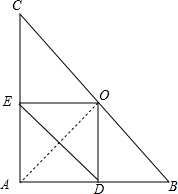 如图,在Rt△ABC中,AB=AC,∠BAC=90°,点O为BC的中点,点D,E分别在AB,AC上滑动且保持BD=AE.在滑动过程中△ODE与△ABC会相似吗?会永远相似吗?请说明你的结论.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,点O为BC的中点,点D,E分别在AB,AC上滑动且保持BD=AE.在滑动过程中△ODE与△ABC会相似吗?会永远相似吗?请说明你的结论.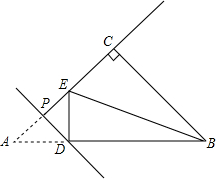 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.
如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.