题目内容
6.已知关于x,y的方程组$\left\{\begin{array}{l}{x+y=-1}\\{ax-y=4}\end{array}\right.$的解满足x-y=3,则a值为2.分析 把x+y=-1,x-y=3联立成方程组,解方程组可得x、y的值,然后把x、y的值代入ax-y=4,再解方程即可.
解答 解:根据题意得:$\left\{\begin{array}{l}{x+y=-1}\\{x-y=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,
将x=1、y=-2代入ax-y=4,得:a-(-2)=4,
解得:a=2,
故答案为:2.
点评 此题主要考查了二元一次方程组的解,当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
5.设a≠b,m≠n,a,b,m,n是已知数,则方程组$\left\{\begin{array}{l}\frac{x}{a+m}+\frac{y}{b+m}=1\\ \frac{x}{a+n}+\frac{y}{b+n}=1\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a+b}\\ y=\frac{(b+m)(b+n)}{a+b}\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=\frac{(a+m)(b+m)}{a-b}\\ y=\frac{(a+n)(b+n)}{a-b}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=-\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ |
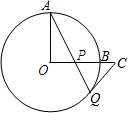 如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.
如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.