题目内容
5.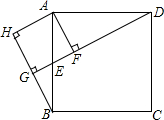 如图,在正方形ABCD中,点E是边AB的中点,过点A作DE的垂线,垂足为F,过点B作DE的垂线,垂足为G,过点A作BG的垂线,垂足为H.求证:四边形AFGH是正方形.
如图,在正方形ABCD中,点E是边AB的中点,过点A作DE的垂线,垂足为F,过点B作DE的垂线,垂足为G,过点A作BG的垂线,垂足为H.求证:四边形AFGH是正方形.
分析 根据垂线的定义,可得∠AFG,∠FGH,∠AHG,根据矩形的判定,可得AHGF的形状,根据余角的性质,可得∠DAF与∠HAB,根据全等三角形的判定与性质,可得AH与AF的关系,根据正方形的定义,可得答案.
解答 证明:∵过点A作DE的垂线,垂足为F,过点B作DE的垂线,垂足为G,过点A作BG的垂线,垂足为H,
∴∠AFG=∠FGH=∠AHG=90°,
∴四边形AFGH是矩形.
∵∠DAF+∠FAE=90°,∠HAB+∠FAE=90°,
∴∠DAF=∠BAH.
∵正方形ABCD,
∴AB=AD.
在△AFD和△AHB中,
$\left\{\begin{array}{l}{∠FAD=∠HAB}\\{∠AFD=∠AHB}\\{AD=AB}\end{array}\right.$,
∴△AFD≌△AHB(AAS),
∴AF=AH,
∴四边形AFGH是正方形.
点评 本题考查了正方形的判定与性质,利用了矩形的判定,全等三角形的判定与性质得出AF=AH是解题关键,又利用了正方形的判定.

练习册系列答案
相关题目
15.已知扇形的圆心角为60°,半径长为12,则扇形的面积为( )
| A. | $\frac{3π}{4}$ | B. | 2π | C. | 3π | D. | 24π |
10.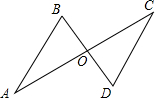 如图所示,△AOB≌△COD,A与C是对应点,那么下列结论中错误的是( )
如图所示,△AOB≌△COD,A与C是对应点,那么下列结论中错误的是( )
 如图所示,△AOB≌△COD,A与C是对应点,那么下列结论中错误的是( )
如图所示,△AOB≌△COD,A与C是对应点,那么下列结论中错误的是( )| A. | ∠B=∠D | B. | ∠AOB=∠COD | C. | AC=BD | D. | AO=CO |