题目内容
9.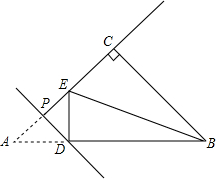 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.
如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.
分析 由翻折变换的性质得到AP=EP,AD=DE,根据已知条件得到AB=6,∠A=45°,于是得到△ADE是等腰直角三角形,当△DEB的两直角边之比为$\frac{1}{2}$时,分两种情况:①当DE:BD=1:2,推出AD:BD=1:2,求得AD=2,于是得到结论;②当DE:BD=2:1,求得AD:BD=2:1,求得AD=4,于是得到AP=$\frac{\sqrt{2}}{2}$AD=2$\sqrt{2}$.
解答 解:由翻折变换的性质得:AP=EP,AD=DE,
∵∠ACB=90°,AC=BC=3$\sqrt{2}$,
∴AB=6,∠A=45°,
∴△ADE是等腰直角三角形,
当△DEB的两直角边之比为$\frac{1}{2}$时,
分两种情况:①当DE:BD=1:2,
∴AD:BD=1:2,
∴AD=2,
∴AP=$\frac{\sqrt{2}}{2}$AD=$\sqrt{2}$.
②当DE:BD=2:1,
∴AD:BD=2:1,
∴AD=4,
∴AP=$\frac{\sqrt{2}}{2}$AD=2$\sqrt{2}$.
综上所述:当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为:2$\sqrt{2}$或$\sqrt{2}$.
故答案为:2$\sqrt{2}$或$\sqrt{2}$.
点评 本题考查了翻折变换的性质、线段垂直平分线的性质、勾股定理、等腰直角三角形的性质;本题有一定难度,需要进行分类讨论.

练习册系列答案
相关题目
5.设a≠b,m≠n,a,b,m,n是已知数,则方程组$\left\{\begin{array}{l}\frac{x}{a+m}+\frac{y}{b+m}=1\\ \frac{x}{a+n}+\frac{y}{b+n}=1\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a+b}\\ y=\frac{(b+m)(b+n)}{a+b}\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=\frac{(a+m)(b+m)}{a-b}\\ y=\frac{(a+n)(b+n)}{a-b}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=-\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ |
6.反比例函数y=(2m-1)${x}^{{m}^{2}-1}$,当x>0时,y随x的增大而增大,则m的值是( )
| A. | ±1 | B. | 小于$\frac{1}{2}$的实数 | C. | -1 | D. | 1 |
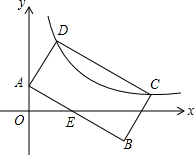 如图,矩形ABCD中,AB=2AD,点A(0,1),点C、D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为$\frac{3+\sqrt{5}}{2}$.
如图,矩形ABCD中,AB=2AD,点A(0,1),点C、D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为$\frac{3+\sqrt{5}}{2}$.