题目内容
15.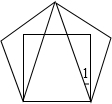 将边长相等的一个正方形与一个正五边形,按如图重叠放置,则∠1度数=18°.
将边长相等的一个正方形与一个正五边形,按如图重叠放置,则∠1度数=18°.
分析 利用多边形内角和公式求得∠E的度数,在等腰三角形AED中可求得∠EAD的度数,进而求得∠BAD的度数,再利用正方形的内角得出∠BAG=90°,进而得出∠DAG的度数.
解答 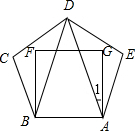 解:∵正五边形ABCDE的内角和为(5-2)×180°=540°,
解:∵正五边形ABCDE的内角和为(5-2)×180°=540°,
∴∠E=$\frac{1}{5}$×540°=108°,∠BAE=108°
又∵EA=ED,
∴∠EAD=$\frac{1}{2}$×(180°-108°)=36°,
∴∠BAD=∠BAE-∠EAD=72°,
∵正方形GABF的内角∠BAG=90°,
∴∠1=90°-72°=18°,
故答案为:18°.
点评 本题考查了正多边形的计算,重点掌握正多边形内角和公式是关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
10.一元二次方程x2+8x-9=0配方后得到的方程是( )
| A. | (x-4)2+7=0 | B. | (x+4)2=25 | C. | (x-4)2=25 | D. | (x+4)2-7=0 |
4.下列各数中,-3的倒数是( )
| A. | 3 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | -3 |
 如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)
如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)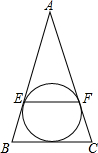 如图,在△ABC中,AB=AC,它的内切圆分别切AB,AC于点E,F,若AB=100,BC=60,求EF的长.
如图,在△ABC中,AB=AC,它的内切圆分别切AB,AC于点E,F,若AB=100,BC=60,求EF的长.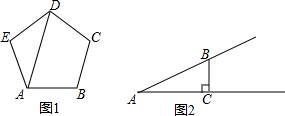
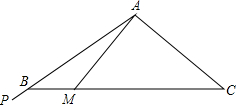 在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm.
在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm.