题目内容
6. 如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)
如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)
分析 阴影部分可看成是圆心角为135°,半径为3是扇形,然后根据扇形的面积公式计算即可.
解答  解:根据图示知,∠1+∠2=180°-90°-45°=45°,
解:根据图示知,∠1+∠2=180°-90°-45°=45°,
∵∠ABC+∠ADC=180°,
∴图中阴影部分的圆心角的和是90°+90°-∠1-∠2=135°,
∴阴影部分的面积应为:S=$\frac{135π×{3}^{2}}{360}$=$\frac{27}{8}$π.
故答案是:$\frac{27}{8}π$.
点评 本题考查扇形的面积的计算.求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.

练习册系列答案
相关题目
11.若a-b=3,则a2-2ab+b2-6的值是( )
| A. | 12 | B. | 6 | C. | 3 | D. | 0 |
16. 如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=( )
如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=( )
 如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=( )
如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.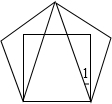 将边长相等的一个正方形与一个正五边形,按如图重叠放置,则∠1度数=18°.
将边长相等的一个正方形与一个正五边形,按如图重叠放置,则∠1度数=18°.