题目内容
3.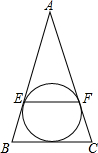 如图,在△ABC中,AB=AC,它的内切圆分别切AB,AC于点E,F,若AB=100,BC=60,求EF的长.
如图,在△ABC中,AB=AC,它的内切圆分别切AB,AC于点E,F,若AB=100,BC=60,求EF的长.
分析 设△ABC的内切圆切BC于点D,连接AD,利用等腰三角形的性质以及切线长定理求出BE=BD=CD=CF=30,再证明△AEF∽△ABC,根据相似三角形的性质得出EF的长.
解答  解:设△ABC的内切圆切BC于点D,连接AD.
解:设△ABC的内切圆切BC于点D,连接AD.
∵AC=AB=100,BC=60,圆O内切于△ABC,切点分别为D、E、F,
∴AD⊥BC,AF=AE,
∴BD=CD=30,BE=BD=CD=CF=30,
∴AE=AF=70,
∵$\frac{AE}{AB}$=$\frac{AF}{AC}$,∠EAF=∠BAC,
∴△AEF∽△ABC,
∴$\frac{EF}{BC}$=$\frac{AE}{AB}$,即$\frac{EF}{60}$=$\frac{70}{100}$,
∴EF=42.
点评 此题主要考查了三角形的内切圆与内心,等腰三角形的性质,切线长定理,相似三角形的性质和判定等知识,根据题意得出AE=AF=70是解题关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13.先化简,再求值:
(1)a(a-4)-(a+6)(a-2),其中a=-$\frac{1}{2}$.
(2)(x+2)2+(2x+1)(2x-1)-4x(x+1),其中x=$\frac{1}{3}$.
(1)a(a-4)-(a+6)(a-2),其中a=-$\frac{1}{2}$.
(2)(x+2)2+(2x+1)(2x-1)-4x(x+1),其中x=$\frac{1}{3}$.
11.若a-b=3,则a2-2ab+b2-6的值是( )
| A. | 12 | B. | 6 | C. | 3 | D. | 0 |
 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)正方形的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A2016的坐标为(504,-504).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)正方形的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A2016的坐标为(504,-504).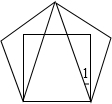 将边长相等的一个正方形与一个正五边形,按如图重叠放置,则∠1度数=18°.
将边长相等的一个正方形与一个正五边形,按如图重叠放置,则∠1度数=18°. 如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C. 观察下列各个等式:
观察下列各个等式: