题目内容
18.为积极开展“六城同创”工作,我市绿化提质改造工程正如火如荼地进行,需要大量的甲、乙两种树苗对滨江路进行绿化改造,某树苗种植户经市场调研发现:如果单独种植甲种树苗,所获利润y甲(万元)与种植亩数x1(亩)之间存在正比例函数关系y甲=kx1,并且当种植5亩时可获利润2万元;如果单独种植乙种树苗,则所获利润y乙(万元)与种植亩数x2(亩)之间存在二次函数关系:y乙=ax22+bx2,且种植2亩时能获利润2.4万元,当种植4亩时,可获利润3.2万元(1)请分别求出上述的正比例函数表达式与二次函数表达式
(2)如果种植户想用10亩地同时种植甲、乙两种树苗,请设计一个能获得最大利润的种植方案,并求出按此方案种植所获得的最大利润是多少?
分析 (1)待定系数法求解可得;
(2)根据题意得W总=y甲+y乙=$\frac{2}{5}$(10-x2)+(-0.2x22+1.6x2)=-0.2x22+1.2x2+4=-0.2(x2-3)2+5.8,据此可得.
解答 解:(1)将x=5、y=2代入y甲=kx1,得:5k=2,
解得:k=$\frac{2}{5}$,
∴y甲=$\frac{2}{5}$x1;
将x=2、y=2.4和x=4、y=3.2代入y乙=ax22+bx2,得:
$\left\{\begin{array}{l}{4a+2b=2.4}\\{16a+4b=3.2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-0.2}\\{b=1.6}\end{array}\right.$,
∴y乙=-0.2x22+1.6x2;
(2)根据题意得:W总=y甲+y乙
=$\frac{2}{5}$(10-x2)+(-0.2x22+1.6x2)
=-0.2x22+1.2x2+4
=-0.2(x2-3)2+5.8,
当x2=3时,W总利润最大为5.8万元,
答:当种植甲种树苗7亩,乙种树苗3亩时,所获利润最大,种植所获得的最大利润为5.8万元.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法求函数解析式及销售问题中的最大利润问题是解题的关键.

练习册系列答案
相关题目
3.当-1≤x≤2时,二次函数y=x2+2mx+m+2,有最小值-3,则实数m的值为( )
| A. | $\frac{1+\sqrt{21}}{2}$或$\frac{1-\sqrt{21}}{2}$ | B. | 6或-$\frac{9}{5}$ | ||
| C. | 6或$\frac{1-\sqrt{21}}{2}$ | D. | 6或-$\frac{9}{5}$或$\frac{1-\sqrt{21}}{2}$或$\frac{1+\sqrt{21}}{2}$ |

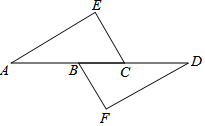 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.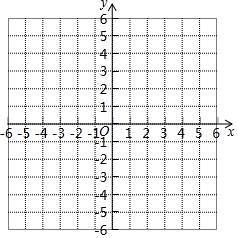 先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)