题目内容
13.如图1,是一种折叠椅,忽略其支架等的宽度,得到它的侧面简化结构图(图2),支架与坐板均用线段表示.若坐板CD平行于地面,前支撑架AB与后支撑架OF分别与CD交于点E,D,ED=25cm,OD=20cm,DF=40cm,∠ODC=60°,∠AED=50°.(1)求两支架着地点B,F之间的距离;
(2)若A、D两点所在的直线正好与地面垂直,求椅子的高度.
(结果取整数,参数数据:sin60°=0.87,cos60°=0.5,tan60°=1.73,sin50°=0.77,cos50°=0.64,tan50°=1.19,可使用科学计算器)

分析 (1)连接BF,过D作DM⊥BF,过E作EN⊥BF于N,于是得到MN=DE=25cm,EN=DM,根据平行线的性质得到∠F=∠ODE=60°,∠B=∠OED=50°,求得EN=DM=20$\sqrt{3}$=34.6,MF=20,由三角函数的定义得到BN=$\frac{EN}{tan50°}$=$\frac{20\sqrt{3}}{1.19}$≈29.08,于是得到结论;
(2)根据三角函数的定义即刻得到结论.
解答 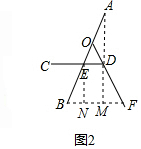 解:(1)连接BF,过D作DM⊥BF,过E作EN⊥BF于N,
解:(1)连接BF,过D作DM⊥BF,过E作EN⊥BF于N,
则MN=DE=25cm,EN=DM,
∵DE∥BF,
∴∠F=∠ODE=60°,∠B=∠OED=50°,
∵DF=40,
∴EN=DM=20$\sqrt{3}$=34.6,MF=20,
∴BN=$\frac{EN}{tan50°}$=$\frac{20\sqrt{3}}{1.19}$≈29.08,
∴BF=BN+MN+MF=74.08cm,
故两支架着地点B,F之间的距离我74.08cm;
(2)在Rt△ADE中,AD=DE•tan50°=29.75cm,
∴AM=29.75+20$\sqrt{3}$≈64cm,
故椅子的高度是64cm.
点评 题主要考查解直角三角形的应用,解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
相关题目
3.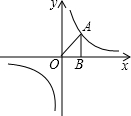 如图,A为反比例函数y=$\frac{k}{x}$图象上一点,AB垂直x轴于B点,若S△AOB=3,则k的值为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上一点,AB垂直x轴于B点,若S△AOB=3,则k的值为( )
 如图,A为反比例函数y=$\frac{k}{x}$图象上一点,AB垂直x轴于B点,若S△AOB=3,则k的值为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上一点,AB垂直x轴于B点,若S△AOB=3,则k的值为( )| A. | 6 | B. | 3 | C. | $\frac{3}{2}$ | D. | 不能确定 |
1.-$\frac{\sqrt{2}}{2}$的绝对值是( )
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
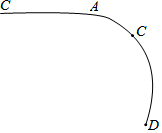 如图,一段圆弧AB上有一个点D,直线AC与圆弧相切于点A,请借助于切点A及B、D两点,利用尺规作图找出这段圆弧所在圆的圆心(不写作法,保留作图痕迹).
如图,一段圆弧AB上有一个点D,直线AC与圆弧相切于点A,请借助于切点A及B、D两点,利用尺规作图找出这段圆弧所在圆的圆心(不写作法,保留作图痕迹).