题目内容
9.多项式2x2-2xy+y2+4x+25的最小值为21.分析 根据完全平方公式把多项式进行变形,根据非负数的性质解答即可.
解答 解:2x2-2xy+y2+4x+25
=x2-2xy+y2+x2+4x+4+21
=(x-y)2+(x+2)2+21,
∵(x-y)2≥0,(x+2)2≥0,
∴(x-y)2+(x+2)2+21≥21,
∴多项式2x2-2xy+y2+4x+25的最小值为21,
故答案为:21.
点评 本题考查的是配方法的应用,掌握完全平方公式、偶次方的非负性是解题的关键.

练习册系列答案
相关题目
1.-$\frac{\sqrt{2}}{2}$的绝对值是( )
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
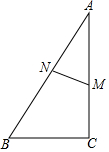 如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.