题目内容
8.如果不等式ax+b>0的解集是x>2,则不等式bx-a<0的解集是x>-$\frac{1}{2}$.分析 不等式ax+b>0的解集是x>2,判断出a>0且-$\frac{b}{a}$=2、b<0,得到$\frac{a}{b}$=-$\frac{1}{2}$;再解出不等式bx-a<0的解集即可.
解答 解:∵不等式ax+b>0的解集是x>2,
∴x>-$\frac{b}{a}$,
则a>0且-$\frac{b}{a}$=2、b<0,
∴$\frac{a}{b}$=-$\frac{1}{2}$
∵bx-a<0,
∴bx<a,
∴x>$\frac{a}{b}$,
∴x>-$\frac{1}{2}$,
故答案为x>-$\frac{1}{2}$.
点评 本题考查了不等式的解集,熟悉不等式的性质是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
3.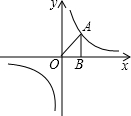 如图,A为反比例函数y=$\frac{k}{x}$图象上一点,AB垂直x轴于B点,若S△AOB=3,则k的值为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上一点,AB垂直x轴于B点,若S△AOB=3,则k的值为( )
 如图,A为反比例函数y=$\frac{k}{x}$图象上一点,AB垂直x轴于B点,若S△AOB=3,则k的值为( )
如图,A为反比例函数y=$\frac{k}{x}$图象上一点,AB垂直x轴于B点,若S△AOB=3,则k的值为( )| A. | 6 | B. | 3 | C. | $\frac{3}{2}$ | D. | 不能确定 |




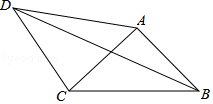 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD2=41.
如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD2=41.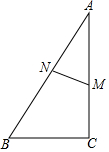 如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.