题目内容
8. 先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)(1)正比例函数y=2x过( 0,0)和( 1,2)
(2)一次函数y=-x+3过( 0,3)和(3,0 )
分析 (1)分别将x=0和x=1代入y=2x中求出与之对应的y值,再描点连线即可画出正比例函数y=2x的图象;
(2)分别将x=0、y=0代入y=-x+3中求出与之对应的y、x的值,再描点连线即可画出一次函数y=-x+3的图象.
解答 解:(1)当x=0时,y=2x=0,
∴正比例函数y=2x过(0,0);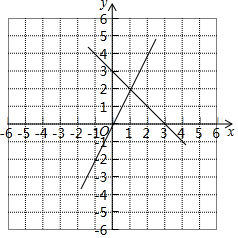
当x=1时,y=2x=1,
∴正比例函数y=2x过(1,2).
故答案为:0;2.
(2)当x=0时,y=-x+3=3,
∴一次函数y=-x+3过(0,3);
当y=0时,有-x+3=0,
解得:x=3,
∴一次函数y=-x+3过(3,0).
故答案为:3;3.
点评 本题考查了正比例函数的图象、一次函数的图象以及一次函数图象上点的坐标特征,解题的关键是:(1)分别将x=0和x=1代入y=2x中求出与之对应的y值;(2)分别将x=0、y=0代入y=-x+3中求出与之对应的y、x的值.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
20.若2x+3=5,则6x+10=( )
| A. | 15 | B. | 16 | C. | 17 | D. | 34 |
 如图,等边△ABC的边长为10,D为AC上任意一点,延长AB至点E,使BE=CD,连接DE交BC于点P.
如图,等边△ABC的边长为10,D为AC上任意一点,延长AB至点E,使BE=CD,连接DE交BC于点P.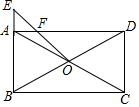 如图,在矩形ABCD中,对角线AC与BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若AB=6,BC=10,AE=2,求AF的长.
如图,在矩形ABCD中,对角线AC与BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若AB=6,BC=10,AE=2,求AF的长.