题目内容
13.某家具商场计划购进某种餐桌、餐椅,有关信息如表:| 原进价(元/张) | 零售价(元/张) | 成套售价(元/张) | |
| 餐桌 | 150 | 270 | 500元 |
| 餐椅 | 40 | 70 |
(2)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(1)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(1)中的最大利润少了2250元.请问本次成套的销售量为多少?
分析 (1)设购进餐桌x张,餐椅(5x+20)张,销售利润为W元.根据购进总数量不超过200张,得出关于x的一元一次不等式,解不等式即可得出x的取值范围,再根据“总利润=成套销售的利润+零售餐桌的利润+零售餐椅的利润”即可得出W关于x的一次函数,根据一次函数的性质即可解决最值问题;
(2)设本次成套销售量为m套,先算出涨价后每张餐桌及餐椅的进价,再根据利润间的关系找出关于m的一元一次方程,解方程即可得出结论.
解答 解:(1)设购进餐桌x张,则购进餐椅(5x+20)张,销售利润为W元.
由题意得:x+5x+20≤200,
解得:x≤30.
∵a=150,
∴餐桌的进价为150元/张,餐椅的进价为40元/张.
依题意可知:
W=$\frac{1}{2}$x•(500-150-4×40)+$\frac{1}{2}$x•(270-150)+(5x+20-$\frac{1}{2}$x•4)•(70-40)=245x+600,
∵k=245>0,
∴W关于x的函数单调递增,
∴当x=30时,W取最大值,最大值为7950.
故购进餐桌30张、餐椅170张时,才能获得最大利润,最大利润是7950元.
(2)涨价后每张餐桌的进价为160元,每张餐椅的进价为50元,
设本次成套销售量为m套.
依题意得:(500-160-4×50)m+(30-m)×(270-160)+(170-4m)×(70-50)=7950-2250,
即6700-50m=5700,
解得:m=20.
答:本次成套的销售量为20套.
点评 本题考查了一次函数的应用、解一元一次不等式、一次函数的性质及解一元一次方程,解题的关键是:(1)根据数量关系找出W关于x的函数解析式;(2)根据数量关系找出关于m的一元一次方程.本题属于中档题,难度不大,但较繁琐,解决该题型题目时,根据数量关系找出函数关系式(方程或方程组)是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | y随x增大而增大 | |
| B. | 图象在第一、三象限 | |
| C. | 当x的绝对值无限增大时,图象能够与x轴相交 | |
| D. | 图象既是轴对称图形又是中心对称图形 |
 如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
 如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )| A. | AD∥BC | B. | ∠B=∠C | C. | ∠2+∠B=180° | D. | AB∥CD |
 如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.
如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.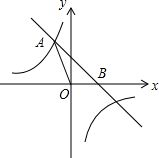 如图,直线y=-x+b与反比例函数$y=-\frac{3}{x}$的图象相交于点A(a,3),且与x轴相交于点B.
如图,直线y=-x+b与反比例函数$y=-\frac{3}{x}$的图象相交于点A(a,3),且与x轴相交于点B.