题目内容
18.解下列方程组(1)$\left\{\begin{array}{l}{3x-y=20}\\{5x+2y=15}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{2s}{3}+\frac{3t}{4}=\frac{1}{2}}\\{\frac{4s}{5}+\frac{5t}{6}=\frac{7}{15}}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-y=20①}\\{5x+2y=15②}\end{array}\right.$,
①×2+②得:11x=55,即x=5,
把x=5代入①点到:y=-5,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=-5}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{8s+9t=6①}\\{24s+25t=14②}\end{array}\right.$,
①×3-②得:2t=4,即t=2,
把t=2代入①得:s=-$\frac{3}{2}$,
则方程组的解为$\left\{\begin{array}{l}{s=-\frac{3}{2}}\\{t=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
9.在下列四个图案中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.某家具商场计划购进某种餐桌、餐椅,有关信息如表:
(1)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和4张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(2)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(1)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(1)中的最大利润少了2250元.请问本次成套的销售量为多少?
| 原进价(元/张) | 零售价(元/张) | 成套售价(元/张) | |
| 餐桌 | 150 | 270 | 500元 |
| 餐椅 | 40 | 70 |
(2)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(1)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(1)中的最大利润少了2250元.请问本次成套的销售量为多少?
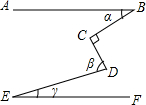 如图,已知AB∥EF,∠C=90°,则α+β-γ=90°.
如图,已知AB∥EF,∠C=90°,则α+β-γ=90°.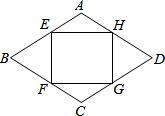 已知如图,在菱形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,AE=AH=CF=CG,求证:四边形EFGH是矩形.
已知如图,在菱形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,AE=AH=CF=CG,求证:四边形EFGH是矩形.