题目内容
2.我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是直角三角形时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是直角三角形或钝角三角形时,它们一定不全等.分析 过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,得出∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,根据SAS证△BDC≌△B1D1C1,推出BD=B1D1,根据HL证Rt△BDA≌Rt△B1D1A1,推出∠A=∠A1,根据AAS推出△ABC≌△A1B1C1即可.
解答  解:已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
解:已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1.
证明:过B作BD⊥AC于D,过B1作B1D1⊥A1C1于D1,
则∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,
在△BDC和△B1D1C1中,
$\left\{\begin{array}{l}{∠C=∠{C}_{1}}\\{∠BDC=∠{B}_{1}{D}_{1}{C}_{1}}\\{BC={B}_{1}{C}_{1}}\end{array}\right.$,
∴△BDC≌△B1D1C1,
∴BD=B1D1,
在Rt△BDA和Rt△B1D1A1中
$\left\{\begin{array}{l}{AB={A}_{1}{B}_{1}}\\{BD={B}_{1}{D}_{1}}\end{array}\right.$,
∴Rt△BDA≌Rt△B1D1A1(HL),
∴∠A=∠A1,
在△ABC和△A1B1C1中
$\left\{\begin{array}{l}{∠C=∠{C}_{1}}\\{∠A=∠{A}_{1}}\\{AB={A}_{1}{B}_{1}}\end{array}\right.$,
∴△ABC≌△A1B1C1(AAS).
同理可得:当这两个三角形都是直角三角形时,它们也会全等,
如图:△ACD与△ACB中,
CD=CB,AC=AC,∠A=∠A,
但:△ACD与△ACB不全等. ,
,
故当这两个三角形其中一个三角形是锐角三角形,另一个是直角三角形或钝角三角形时,它们一定不全等.
故答案为:直角三角形,直角三角形或钝角三角形.
点评 本题考查了全等三角形像的判定;SSA不能判定的原因是有锐角钝角三角形不能全等,把三角形分类后就能全等了.

| A. | y=5x+1 | B. | y=5x+9 | C. | y=$\frac{1}{5}$x-$\frac{9}{5}$ | D. | y=$\frac{1}{5}$x+$\frac{1}{5}$ |
| 原进价(元/张) | 零售价(元/张) | 成套售价(元/张) | |
| 餐桌 | 150 | 270 | 500元 |
| 餐椅 | 40 | 70 |
(2)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(1)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(1)中的最大利润少了2250元.请问本次成套的销售量为多少?
| A. | 1 | B. | 0 | C. | -1 | D. | 1或-1 |
| A. | 6 | B. | 8 | C. | 2$\sqrt{7}$ | D. | 10 |
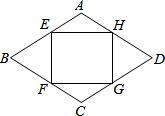 已知如图,在菱形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,AE=AH=CF=CG,求证:四边形EFGH是矩形.
已知如图,在菱形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,AE=AH=CF=CG,求证:四边形EFGH是矩形.