题目内容
3. 如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.
如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.(1)求证:AB=CD;
(2)求证:DP•BD=AD•BC.
分析 (1)利用平行线的性质结合圆周角定理得出$\widehat{AB}=\widehat{DC}$,进而得出答案;
(2)首先得出△ADP∽△DBC,进而利用相似三角形的性质得出答案.
解答 证明:(1)∵AD∥BC,
∴∠ADB=∠DBC,
∴$\widehat{AB}=\widehat{DC}$,
∴AB=CD;
(2)∵∠APB=∠BAD,∠BAD+∠BCD=180°,∠APB+∠APD=180°,
∴∠BCD=∠APD,
∵∠ADB=∠CBD,
∴△ADP∽△DBC,
∴$\frac{AD}{BD}=\frac{DP}{BC}$,
∴DP•BD=AD•BC.
点评 此题主要考查了相似三角形的判定与性质、平行线的性质、圆周角定理等知识;熟练应用相似三角形的判定与性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.从方程组$\left\{\begin{array}{l}{x={m}^{2}-1}\\{y=5{m}^{2}+4}\end{array}\right.$中得出x与y的关系是( )
| A. | y=5x+1 | B. | y=5x+9 | C. | y=$\frac{1}{5}$x-$\frac{9}{5}$ | D. | y=$\frac{1}{5}$x+$\frac{1}{5}$ |
13.某家具商场计划购进某种餐桌、餐椅,有关信息如表:
(1)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和4张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(2)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(1)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(1)中的最大利润少了2250元.请问本次成套的销售量为多少?
| 原进价(元/张) | 零售价(元/张) | 成套售价(元/张) | |
| 餐桌 | 150 | 270 | 500元 |
| 餐椅 | 40 | 70 |
(2)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(1)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(1)中的最大利润少了2250元.请问本次成套的销售量为多少?
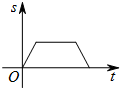
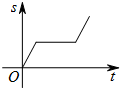
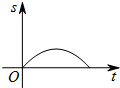
 如图,一只蚂蚁从O点出发,在扇形AOB的边缘沿着O-A-B-O的路线匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
如图,一只蚂蚁从O点出发,在扇形AOB的边缘沿着O-A-B-O的路线匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )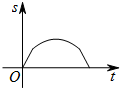
 如图,正方形ABCD中,E为对角线AC上一点,连结EB、ED,延长BE交AD于点F.
如图,正方形ABCD中,E为对角线AC上一点,连结EB、ED,延长BE交AD于点F.