��Ŀ����
14��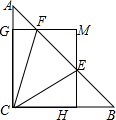 ��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC=1��E��F���߶�AB�ϵ��������㣬�ҡ�ECF=
��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC=1��E��F���߶�AB�ϵ��������㣬�ҡ�ECF=45�㣬����E��F�ֱ���BC��AC�Ĵ����ཻ�ڵ�M������ֱ�ΪH��G�������жϣ�
��AB=$\sqrt{2}$���ڵ���E���B�غ�ʱ��MH=$\frac{1}{2}$����$\frac{AE}{BC}$=$\frac{AC}{BF}$����AF+BE=EF��
������ȷ�Ľ����У�������
| A�� | �٢ڢ� | B�� | �٢ۢ� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
���� ��������֪����ABC�ǵ���ֱ�������Σ����ݵ���ֱ�������μ��������жϣ�
����ͼ1������E���B�غ�ʱ����H���B�غϣ��ɵ�MG��BC���ı���MGCB�Ǿ��Σ���һ���õ�FG�ǡ�ACB����λ�ߣ��Ӷ������жϣ�
�۸���������ȿ�֤��ACE�ס�BFC��
����ͼ2��ʾ��SAS��֤��ECF�ա�ECD������ȫ�������ε����ʺ��ɶ������������жϣ�
��� �⣺��������֪����ABC�ǵ���ֱ�������Σ�
��AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2}$���ʢ���ȷ��
����ͼ1������E���B�غ�ʱ����H���B�غϣ�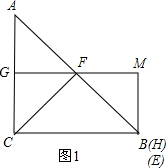
��MB��BC����MBC=90�㣬
��MG��AC��
���MGC=90��=��C=��MBC��
��MG��BC���ı���MGCB�Ǿ��Σ�
��MH=MB=CG��
�ߡ�FCE=45��=��ABC����A=��ACF=45�㣬
��CF=AF=BF��
��FG�ǡ�ACB����λ�ߣ�
��GC=$\frac{1}{2}$AC=MH���ʢ���ȷ��
����ͼ2��ʾ��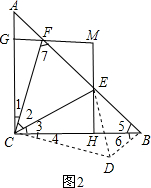
��AC=BC����ACB=90�㣬
���A=��5=45�㣮
����ACF˳ʱ����ת90������BCD��
��CF=CD����1=��4����A=��6=45�㣻BD=AF��
�ߡ�2=45�㣬
���1+��3=��3+��4=45�㣬
���DCE=��2��
�ڡ�ECF�͡�ECD�У�
$\left\{\begin{array}{l}{CF=CD}\\{��2=��DCE}\\{CE=CE}\end{array}\right.$��
���ECF�ա�ECD��SAS����
��EF=DE��
�ߡ�5=45�㣬
���DBE=90�㣬
��DE2=BD2+BE2����EF2=AF2+BE2���ʢܴ���
�ۡߡ�7=��1+��A=��1+45��=��1+��2=��ACE��
�ߡ�A=��5=45�㣬
���ACE�ס�BFC��
��$\frac{AE}{BC}$=$\frac{AC}{BF}$��
�ʢ���ȷ��
��ѡA��
���� ���⿼�����������ۺ��⣬�漰��֪ʶ���У�����ֱ�������ε��ж������ʣ�ƽ���ߵ��ж������ʣ����ε��ж������ʣ���������λ�ߵ����ʣ�ȫ�������ε��ж������ʣ����ɶ��������������ε��ж������ʣ��ۺ��Խ�ǿ����һ�����Ѷȣ�

 ��ͼ��һ���ִ���B���۲����Aλ����ƫ��50�㷽���ϣ����40����ִ���B������ƫ��20�㷽�����ٺ�����C������C���۲����Aλ�ڱ�ƫ��10�㷽���ϣ���C�������A�ľ����ǣ�������
��ͼ��һ���ִ���B���۲����Aλ����ƫ��50�㷽���ϣ����40����ִ���B������ƫ��20�㷽�����ٺ�����C������C���۲����Aλ�ڱ�ƫ��10�㷽���ϣ���C�������A�ľ����ǣ�������| A�� | 20���� | B�� | 40���� | C�� | 20$\sqrt{3}$���� | D�� | 40$\sqrt{3}$���� |
 ��ͼ�����Ϻ�ij����A����һ�Ҳ��㴬����ҵʱͻ���ش���ˣ������������ҹ������Ѿ����ķ�������źţ���ʱһ����������Ѳ�������㴬��������25�����B�������������յ������������ָ���ǰȥ��Ԯ��������֮���д�Ƭ��������ֱ�ߵ�����Ǿ������ϵ�����������ƫ��60�㷽����ÿСʱ40������ٶȺ��а�Сʱ����C����������ƫ��53�㷽���У�ͬʱ���㴬������������ٺ��У����������ٲ��䣬������D����ϣ���CD����ľ���Ͳ��㴬���ٶȣ����������������
��ͼ�����Ϻ�ij����A����һ�Ҳ��㴬����ҵʱͻ���ش���ˣ������������ҹ������Ѿ����ķ�������źţ���ʱһ����������Ѳ�������㴬��������25�����B�������������յ������������ָ���ǰȥ��Ԯ��������֮���д�Ƭ��������ֱ�ߵ�����Ǿ������ϵ�����������ƫ��60�㷽����ÿСʱ40������ٶȺ��а�Сʱ����C����������ƫ��53�㷽���У�ͬʱ���㴬������������ٺ��У����������ٲ��䣬������D����ϣ���CD����ľ���Ͳ��㴬���ٶȣ����������������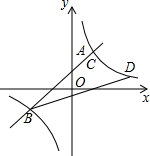 ��ͼ��һ�κ���y=kx+1��k��0����ͼ���뷴��������y=$\frac{m}{x}$��m��0����ͼ����A��B���㣬���е�A������Ϊ��1��2����ֱ��l��x���ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�C��D��
��ͼ��һ�κ���y=kx+1��k��0����ͼ���뷴��������y=$\frac{m}{x}$��m��0����ͼ����A��B���㣬���е�A������Ϊ��1��2����ֱ��l��x���ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�C��D��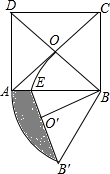 ��ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB�Ƶ�B��ʱ����ת60��õ���BO��B�䣬AB�뻡OO���ཻ�ڵ�E����AD=2����ͼ����Ӱ���ֵ������$\frac{2��}{3}$-$\frac{\sqrt{6}}{2}$��
��ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB�Ƶ�B��ʱ����ת60��õ���BO��B�䣬AB�뻡OO���ཻ�ڵ�E����AD=2����ͼ����Ӱ���ֵ������$\frac{2��}{3}$-$\frac{\sqrt{6}}{2}$��