题目内容
8.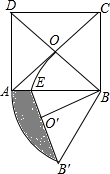 如图,在正方形ABCD中,对角线AC、BD相交于点O,△AOB绕点B逆时针旋转60°得到△BO′B′,AB与弧OO′相交于点E,若AD=2,则图中阴影部分的面积是$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.
如图,在正方形ABCD中,对角线AC、BD相交于点O,△AOB绕点B逆时针旋转60°得到△BO′B′,AB与弧OO′相交于点E,若AD=2,则图中阴影部分的面积是$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.
分析 由旋转得到∠B′BE=60°,BE=BO,BB′=AB,求出S扇形ABB′和S△BB′E即可.
解答 解:由题意可得,BB′=BA=AD=2,
∴BO=$\frac{1}{2}BD=\frac{1}{2}×\sqrt{A{D}^{2}+A{B}^{2}}$=$\frac{1}{2}×\sqrt{{2}^{2}+{2}^{2}}=\sqrt{2}$,
∴BO′=$\sqrt{2}$,
由旋转有,∠B′BE=60°,BE=BO,BB′=AB
S△BB′E=$\frac{1}{2}$BE×BB′SIN∠B′BE=$\frac{1}{2}$×$\sqrt{2}$×2×sin60°=$\frac{\sqrt{6}}{2}$,
S扇形ABB′=$\frac{60×π{×AB}^{2}}{360}$=$\frac{2π}{3}$,
∴S阴影=S扇形ABB′-S△BB′E=$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.
故答案为$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.
点评 此题是旋转和扇形面积的简单综合题,主要考查了旋转的性质和扇形面积的计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一、阅读理解:
一、阅读理解: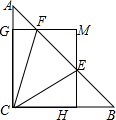 如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=
如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=
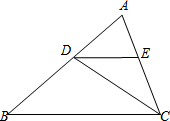 如图所示,已知△ABC中,AB=2,D在AB边上移动(不与A、B重合),DE∥BC交AC于E,连CD.设S△ABC=S,S△DEC=S1.
如图所示,已知△ABC中,AB=2,D在AB边上移动(不与A、B重合),DE∥BC交AC于E,连CD.设S△ABC=S,S△DEC=S1.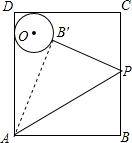 如图,矩形ABCD中,AB=20,AD=25,矩形内有一点O,以O为圆心,5为半径画圆,与AD,CD都相切,点P是BC上一点,将△ABP沿着AP对折得到△AB′P,若AB′与⊙O相切于点B′.则BP的长度是12.
如图,矩形ABCD中,AB=20,AD=25,矩形内有一点O,以O为圆心,5为半径画圆,与AD,CD都相切,点P是BC上一点,将△ABP沿着AP对折得到△AB′P,若AB′与⊙O相切于点B′.则BP的长度是12.