题目内容
2. 如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向25海里的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时40海里的速度航行半小时到达C处,再向南偏东53°方向航行,同时捕鱼船向正北方向低速航行.若两船航速不变,并且在D处会合,求CD两点的距离和捕鱼船的速度(结果保留整数).
如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向25海里的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时40海里的速度航行半小时到达C处,再向南偏东53°方向航行,同时捕鱼船向正北方向低速航行.若两船航速不变,并且在D处会合,求CD两点的距离和捕鱼船的速度(结果保留整数).(参考数据:$\sqrt{3}$≈1.7,sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)
分析 首先过点C作CG⊥AB于点G,过点D作DF⊥CG于点F,在Rt△CBG中,由题意知∠CBG=30°,可求得CG与BG的长,易得四边形ADFG是矩形,然后在Rt△CDF中,∠CFD=90°,∠DCF=53°,可求得CD的长,继而求得AD的长,则可求得答案.
解答 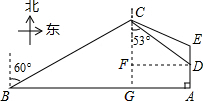 解:如图,过点C作CG⊥AB于点G,过点D作DF⊥CG于点F,
解:如图,过点C作CG⊥AB于点G,过点D作DF⊥CG于点F,
在Rt△CBG中,由题意知∠CBG=30°,
∴CG=$\frac{1}{2}$BC=$\frac{1}{2}$×40×$\frac{1}{2}$=10(海里),BG=BC•cos30°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$≈17(海里),
∵∠DAG=90°,
∴四边形ADFG是矩形,
∴DF=AG=AB-BG=25-17=8(海里),
在Rt△CDF中,∠CFD=90°,
∵∠DCF=53°,
∴CD=$\frac{DF}{sin53°}$≈10(海里).CF=$\frac{DF}{tan53°}$≈6(海里),
∴AD=FG=CG-CF=10-6=4(海里),
∵渔政船航行时间为:$\frac{1}{2}$+$\frac{10}{40}$=$\frac{3}{4}$(小时),
∴捕鱼船的速度为:4÷$\frac{3}{4}$≈5(海里/时).
答:CD两点的距离约为10海里,捕鱼船的速度约为5海里/时.
点评 此题考查了方向角问题.注意准确构造直角三角形是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
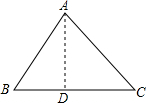
7. 如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )
如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )
 如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )
如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )| A. | C与D | B. | A与B | C. | A与C | D. | B与C |
 一、阅读理解:
一、阅读理解: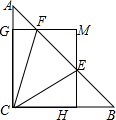 如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=
如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=