题目内容
19.(1)解方程组$\left\{\begin{array}{l}{4x-3y=2①}\\{2x+y=6②}\end{array}\right.$(2)先化简,再求值:(2a-b)(b+2a)-(a-2b)2+5b2,其中a=-1,b=2.
分析 (1)利用解方程组的方法与步骤求得未知数的值即可;
(2)先利用平方差公式和完全平方公式计算合并,再进一步代入求得答案即可.
解答 解:(1)$\left\{\begin{array}{l}{4x-3y=2①}\\{2x+y=6②}\end{array}\right.$
②×2-①得5y=10,
解得y=2,
把y=2代入②得x=2,
所以原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
(2)原式=4a2-b2-a2+4ab-4b2+5b2,
=3a2+4ab
当a=-1,b=2时,
原式=3×(-1)2+4×(-1)×2=-5.
点评 此题考查了解二元一次方程组,整式的混合运算-化简求值,熟练掌握运算法则与解答步骤是解本题的关键.

练习册系列答案
相关题目
9.某件商品,按成本价提高40%后标价,又以8折优惠卖出,结果仍可获利15元,则这件商品的成本价为( )
| A. | 115元 | B. | 120元 | C. | 125元 | D. | 150元 |
7. 如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )
如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )
 如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )
如图,表示$\sqrt{8}$的点在数轴上表示时,所在哪两个字母之间( )| A. | C与D | B. | A与B | C. | A与C | D. | B与C |
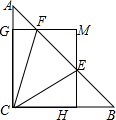 如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=
如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=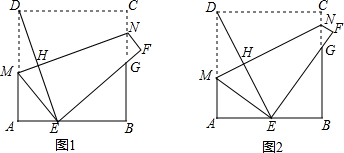
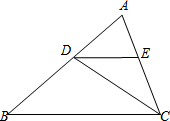 如图所示,已知△ABC中,AB=2,D在AB边上移动(不与A、B重合),DE∥BC交AC于E,连CD.设S△ABC=S,S△DEC=S1.
如图所示,已知△ABC中,AB=2,D在AB边上移动(不与A、B重合),DE∥BC交AC于E,连CD.设S△ABC=S,S△DEC=S1.