Question

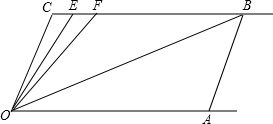如图，OC∥AB，∠C=∠OAB=100°，E、F在CB上，OB平分∠FOA，OE平分∠COF，∠EOB=40°．
（1）求证：CB∥OA；
（2）若左右平行移动AB，则∠OBC：∠OFC的值是否发生变化？若变化，找出变化规律；若不变，求比值；
（3）在平行移动AB的过程中，是否存在某种情况使∠OEC=∠OBA？若存在，求∠OEC的度数；若不存在，请说明理由．

Answer 1

考点：平行线的判定与性质

专题：计算题

分析：（1）由CO与OA平行，利用两直线平行同旁内角互补求出∠COA度数，根据OB平分∠FOA，OE平分∠COF，得到∠FOB=∠AOB，∠COE=∠FOE，进而得到∠COA=2∠EOB=80°，得到一对同旁内角互补，利用同旁内角互补两直线平行即可得证；
（2）∠OBC：∠OFC的值不变化，理由为：由CB与OA平行，利用两直线平行内错角相等得到∠CBO=∠BOA，再由OB为角平分线得到一对角相等，等量代换得到∠FOB=∠OBC，再由∠FOB+∠OBC=∠OFC，得到∠OFC=2∠OBC，即可得证；
（3）存在某种情况，使∠OEC=∠OBA，此时∠OEC=∠OBA=60°，理由如下：在三角形COE与三角形AOB中，利用内角和定理列出两个等式，得到∠COE=∠BOA，根据∠FOB=∠AOB，且OE平分∠COF，得到∠BOA=∠BOF=∠FOE=∠EOC=∠COA=20°，即可求出∠OEC=∠OBA=60°．

解答：解：（1）∵CO∥OA，∠C=∠OAB=100°，
∴∠COA=180°-100°=80°，
又∵E、F在CB上，OB平分∠FOA，OE平分∠COF，即∠FOB=∠AOB，∠COE=∠FOE，∠EOB=40°，
∴∠COA=2∠EOB=80°，
∴∠C+∠COA=180°，
∴CB∥OA；
（2）不变，
∵CB∥OA，
∴∠CBO=∠BOA，
又∵∠FOB=∠AOB，
∴∠FOB=∠OBC，
∵∠FOB+∠OBC=∠OFC，即∠OFC=2∠OBC，
∴∠OBC：∠OFC=1：2；
（3）存在某种情况，使∠OEC=∠OBA，此时∠OEC=∠OBA=60°，理由如下：
∵∠COE+∠CEO+∠C=180°，∠BOA+∠OAB+∠ABO=180°，且∠OEC=∠OBA，∠C=∠OAB=100°，
∴∠COE=∠BOA，
又∵∠FOB=∠AOB，OE平分∠COF，
∴∠BOA=∠BOF=∠FOE=∠EOC=∠COA=20°，
∴∠OEC=∠OBA=60°．

点评：此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关键．