题目内容

一个扇形的面积是3.14平方米，半径为2米，这个扇形周长是
 
．
考点：扇形面积的计算,弧长的计算
专题：
分析：先求扇形的弧长l，再利用扇形周长为：2R+l计算即可．
解答：解：设此扇形的弧长为l，
∵一个扇形的面积是3.14平方米，半径为2米，
∴
1
2
l×2=3.14，
∴l=3.14，
∴这个扇形的周长为：2R+l=2×2+3.14=7.14米．
故答案为7.14米．
点评：本题主要考查了弧长的计算及扇形的面积公式的应用，利用扇形的面积计算其弧长是解决本题的关键，属基础题．
练习册系列答案
相关题目
化简求值：[（2xy-1）2-2（xy-1）（1+xy）-3]÷2y，其中x=-2，y=-3．
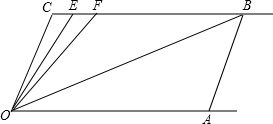如图，OC∥AB，∠C=∠OAB=100°，E、F在CB上，OB平分∠FOA，OE平分∠COF，∠EOB=40°．
（1）求证：CB∥OA；
（2）若左右平行移动AB，则∠OBC：∠OFC的值是否发生变化？若变化，找出变化规律；若不变，求比值；
（3）在平行移动AB的过程中，是否存在某种情况使∠OEC=∠OBA？若存在，求∠OEC的度数；若不存在，请说明理由．
将长度为12cm的线段截成两条线段a、b（a、b长度均为整数），如果截成的a、b长度分别相同算作同一种截法（如：a=9，b=1和a=1，b=9为同一种截法），那么以截成的a、b为对角线，以另一条c=4cm长的线段为一边，能构成平行四边形的概率是
 
．
如图，在半径为
5
2
的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=4，则OP的长为
 
．
代数式（x-1）-1成立的x的取值范围是
 
．
如图，在3×3的方格内，填写了一些式子和数，若图中各行、各列和对角线上三个数之和都相等，则x的值为
 
．
已知⊙O1和⊙O2的半径分别是2cm和3cm，若O1O2=1cm，则⊙O1和⊙O2的位置关系是
 
．
若不等式组
x＞-2
x＞m+2
的解集是x＞-1，则m的值是（　　）
A、-1＜m＜1B、-1或-3
C、-1D、-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网