题目内容
奉化水蜜桃被誉为“琼浆玉露,瑶池珍品”.现有若干个水蜜桃要分给一群同学,如果每人分一个,那么桃子多出30个;如果每人分三个,那么有一人分到了桃子但不足3个.则这群学生有 人.
考点:一元一次不等式组的应用
专题:
分析:设这群学生有x人,如果每人分一个,那么桃子多出30个;桃子数量为x+30;再根据如果每人分三个,那么有一人分到了桃子但不足3个列出不等式组解决问题.
解答:解:设这群学生有x人,根据题意列不等式组得,
,
解得:15<x<16.5,
∵x只能取整数,
∴x=16;
答:这群学生有16人.
故答案为:16.
|
解得:15<x<16.5,
∵x只能取整数,
∴x=16;
答:这群学生有16人.
故答案为:16.
点评:此题考查了一元一次不等式组的应用,关键是读懂题意,找出题目中的数量关系,列出不等式组,要注意x只能取整数.

练习册系列答案
相关题目
若不等式组
的解集是x>-1,则m的值是( )
|
| A、-1<m<1 | B、-1或-3 |
| C、-1 | D、-3 |
 观察如图,图中直线的数量是( )
观察如图,图中直线的数量是( )| A、1条 | B、2条 |
| C、3条 | D、以上都不对 |
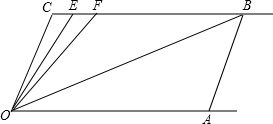 如图,OC∥AB,∠C=∠OAB=100°,E、F在CB上,OB平分∠FOA,OE平分∠COF,∠EOB=40°.
如图,OC∥AB,∠C=∠OAB=100°,E、F在CB上,OB平分∠FOA,OE平分∠COF,∠EOB=40°. 如图,在3×3的方格内,填写了一些式子和数,若图中各行、各列和对角线上三个数之和都相等,则x的值为
如图,在3×3的方格内,填写了一些式子和数,若图中各行、各列和对角线上三个数之和都相等,则x的值为 如图,已知⊙O半径为9cm,射线PM经过点O,OP=15cm,射线PN与⊙O相交于点Q,动点A自P点以
如图,已知⊙O半径为9cm,射线PM经过点O,OP=15cm,射线PN与⊙O相交于点Q,动点A自P点以