题目内容
操作与探究
(1)如图1,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.①画出△AB′C′;②点C′的坐标 .B′C′的长度为
(2)如图2,在平面直角坐标系中,函数y=-x的图象l是第二、四象限的角平分线.
实验与探究:
由图观察易知A(0,2)关于直线l的对称点A′的坐标为(-2,0),请在图中分别标明B(4,3)、C(-2,4)关于直线l的对称点B′、C′的位置,并写出它们的坐标:B′ 、C′ ;
归纳与发现:
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第二、四象限的角平分线l的对称点P′的坐标为 .

(1)如图1,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.①画出△AB′C′;②点C′的坐标
(2)如图2,在平面直角坐标系中,函数y=-x的图象l是第二、四象限的角平分线.
实验与探究:
由图观察易知A(0,2)关于直线l的对称点A′的坐标为(-2,0),请在图中分别标明B(4,3)、C(-2,4)关于直线l的对称点B′、C′的位置,并写出它们的坐标:B′
归纳与发现:
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第二、四象限的角平分线l的对称点P′的坐标为

考点:一次函数综合题
专题:
分析:(1)根据旋转变换的性质得出对应点B′,C′位置,进而利用勾股定理得出答案;
(2)利用网格结合轴对称的性质得出对应点位置进而得出答案.
(2)利用网格结合轴对称的性质得出对应点位置进而得出答案.
解答:解:(1)如图1所示: 点C′的坐标为:(-2,5),
点C′的坐标为:(-2,5),
B′C′的长度为:
;
(2)如图2,
如图所示:
B′(-3,-4)、C′(-4,2);
∵B(4,3),C(-2,4),
∴坐标平面内任一点P(m,n)关于第二、四象限的角平分线l的对称
点P′的坐标为:(-n,-m).
故答案为:(-3,-4),(-4,2),(-n,-m).
 点C′的坐标为:(-2,5),
点C′的坐标为:(-2,5),B′C′的长度为:
| 5 |
(2)如图2,
如图所示:
B′(-3,-4)、C′(-4,2);
∵B(4,3),C(-2,4),
∴坐标平面内任一点P(m,n)关于第二、四象限的角平分线l的对称
点P′的坐标为:(-n,-m).
故答案为:(-3,-4),(-4,2),(-n,-m).
点评:本题考查的是图形旋转变换以及一次函数综合题,涉及到关于直线y=-x的点的坐标特点问题等知识,难度适中.

练习册系列答案
相关题目

 如图,AB是⊙O的直径,EF是⊙O的切线,切点是C,点D是EF上一个动点,连接AD.试探索点D运动到什么位置时,AC是∠BAD的平分线,请说明理由.
如图,AB是⊙O的直径,EF是⊙O的切线,切点是C,点D是EF上一个动点,连接AD.试探索点D运动到什么位置时,AC是∠BAD的平分线,请说明理由.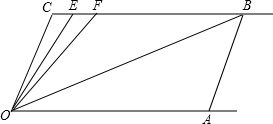 如图,OC∥AB,∠C=∠OAB=100°,E、F在CB上,OB平分∠FOA,OE平分∠COF,∠EOB=40°.
如图,OC∥AB,∠C=∠OAB=100°,E、F在CB上,OB平分∠FOA,OE平分∠COF,∠EOB=40°. 如图,在半径为
如图,在半径为