题目内容
 如图.AB为⊙O的直径,CP为⊙O的切线与BA的延长线交于点P.
如图.AB为⊙O的直径,CP为⊙O的切线与BA的延长线交于点P.(1)求证:∠ACP=∠B;
(2)试证明:PC2=PA•PB.
考点:切线的性质,相似三角形的判定与性质
专题:证明题
分析:(1)连接OC,由切线的性质可知:OC⊥CP,所以∠OCP=90°,所以∠ACP+∠OCA=90°,再利用圆的半径相等和圆周角定理即可证明:∠ACP=∠B;
(2)由(1)可知:∠ACP=∠B,再由条件∠P=∠P,所以可证明:△ACP∽△CBP,由相似三角形的性质:对应边的比值相等即可证明:PC2=PA•PB.
(2)由(1)可知:∠ACP=∠B,再由条件∠P=∠P,所以可证明:△ACP∽△CBP,由相似三角形的性质:对应边的比值相等即可证明:PC2=PA•PB.
解答:证明:(1)连接OC,
∵CP为⊙O的切线,
∴OC⊥CP,
∴∠OCP=90°,
∴∠ACP+∠OCA=90°,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC+∠ACP=90°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B+∠OAC=90°,
∴∠ACP=∠B;
(2)∵∠ACP=∠B,∠P=∠P,
∴△ACP∽△CBP,
∴PC:PB=AP:PC,
∴PC2=PA•PB.

∵CP为⊙O的切线,
∴OC⊥CP,
∴∠OCP=90°,
∴∠ACP+∠OCA=90°,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC+∠ACP=90°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B+∠OAC=90°,
∴∠ACP=∠B;
(2)∵∠ACP=∠B,∠P=∠P,
∴△ACP∽△CBP,
∴PC:PB=AP:PC,
∴PC2=PA•PB.
点评:本题考查了圆周角定理、切线的性质、相似三角形的判定和性质,解题的关键是连接OC利用切线的性质构造直角三角形,是中考常见题型.

练习册系列答案
相关题目
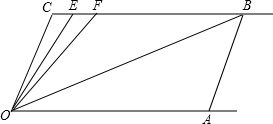 如图,OC∥AB,∠C=∠OAB=100°,E、F在CB上,OB平分∠FOA,OE平分∠COF,∠EOB=40°.
如图,OC∥AB,∠C=∠OAB=100°,E、F在CB上,OB平分∠FOA,OE平分∠COF,∠EOB=40°. 如图,在半径为
如图,在半径为 如图,在3×3的方格内,填写了一些式子和数,若图中各行、各列和对角线上三个数之和都相等,则x的值为
如图,在3×3的方格内,填写了一些式子和数,若图中各行、各列和对角线上三个数之和都相等,则x的值为