题目内容
10.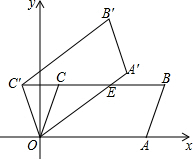 如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为5.
如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为5.
分析 过点C作CD⊥OC′于点D.利用旋转的性质和面积法求得CD的长,然后通过解直角三角形推知:tan∠COC′=$\frac{3}{4}$.结合图形和旋转的性质得到∠COC′=∠AOE,自点E向x轴引垂线,交x轴于点F,则EF=3.利用等角的正切值相等tan∠AOE=tan∠COC′=$\frac{EF}{OF}$=$\frac{3}{4}$,进而求得OF的长度,则C′E=O′E+O′C=4+1=5.
解答  解:∵OC=OC′,CC′⊥y轴,A,B的坐标分别为(6,0),(7,3),
解:∵OC=OC′,CC′⊥y轴,A,B的坐标分别为(6,0),(7,3),
∴点C到y轴的距离:7-6=1.
∴O′C=O′C′=1,O点到CC′的距离是3,
∴OC=OC′=$\sqrt{10}$,S△OCC′=$\frac{1}{2}$×2×3=3.
如图,过点C作CD⊥OC′于点D,则$\frac{1}{2}$OC′•CD=3,
∴CD=$\frac{6}{\sqrt{10}}$,sin∠COC′=$\frac{CD}{OC}$=$\frac{3}{5}$,tan∠COC′=$\frac{3}{4}$.
∵∠COC′+∠COE=∠AOE+∠COE,
∴∠COC′=∠AOE,
∴tan∠AOE=tan∠COC′=$\frac{3}{4}$.
如图,过E作x轴的垂线,交x轴于点F,则EF=OO'=3.
∵tan∠AOE=$\frac{EF}{OF}$,
∴OF=$\frac{EF}{tan∠AOE}$=4,
∵OF=O′E=4,
∴C′E=O′E+O′C′=4+1=5.
故答案为:5.
点评 本题考查了平行四边形的性质和旋转的性质,根据题意作出辅助线是解题的关键与难点,解题时注意面积法的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.根据下列条件,能判定△ABC≌△DEF的是( )
| A. | AB=DE,BC=EF,∠A=∠D | B. | ∠A=∠D,∠C=∠F,AC=DF | ||
| C. | ∠B=∠E,∠A=∠D,AC=EF | D. | AB=DE,BC=EF,∠B=∠D |
 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图. 小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线:
小米是一个爱动脑筋的孩子,他用如下方法作∠AOB的角平分线: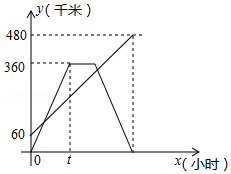 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题: