题目内容
20. 如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.(1)画出将△ABC向右平移2个单位得到△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2;
(3)把△A2B2C2沿着x轴翻折得到△A3B3C3,判断点C与点C3是否在同一个反比例函数的图象上,说明理由.
分析 (1)将点A、B、C分别向右平移2个单位得到其对应点,顺次连接即可得;
(2)将点A、B、C分别绕点O顺时针方向旋转90°得到其对应点,顺次连接即可得;
(3)由翻折性质得出点C3的坐标,根据横纵坐标乘积是否相等即可判断.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)C(-3,2),C3(2,-3),
∵-3×2=2×(-3)=-6,
∴点C,C3都在双曲线y=$-\frac{6}{x}$上.
点评 本题主要考查平移变换、旋转变换及翻折变换,熟练掌握平移变换、旋转变换及翻折变换的定义和性质是解题的关键.

练习册系列答案
相关题目
9.为解决“最后一公里”的交通接驳问题,平谷区投放了大量公租自行车供市民使用.据统计,目前我区共有公租自行车3 500辆.将3 500用科学记数法表示应为( )
| A. | 0.35×104 | B. | 3.5×103 | C. | 3.5×102 | D. | 35×102 |
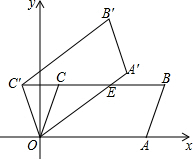 如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为5.
如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为5.