题目内容
20．
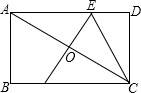如图，在?ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则△CDE的周长为（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 12 |
分析 根据线段垂直平分线的性质可得AE=EC，再根据平行四边形的性质可得AD=4，DC=2，进而可得答案．
解答 解：∵对角线AC的垂直平分线分别交AD、AC于点E、O，
∴AE=CE，
∵四边形ABCD是平行四边形，
∴AD=BC=4，DC=AB=2
∴ED+AE=ED+EC=4，
∴△CDE的周长为4+2=6，
故选：B．
点评 此题主要考查了平行四边形的性质和线段垂直平分线的性质，关键是掌握垂直平分线上任意一点，到线段两端点的距离相等，平行四边形对边相等．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
11．
如图，点D在AC的垂直平分线上，AB∥CD．若∠BAC=25°，则∠D的度数是（ ）
如图，点D在AC的垂直平分线上，AB∥CD．若∠BAC=25°，则∠D的度数是（ ）| A． | 120° | B． | 130° | C． | 140° | D． | 150° |
8．某商场欲购进果汁饮料和碳酸饮料共150箱，两种饮料每箱的进价和售价如下表所示．设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为w元（注：总利润=总售价-总进价）．
（1）设购进碳酸饮料y箱，直接写出y与x的函数关系式为y=150-x；
（2）求总利润w关于x的函数关系式；
（3）如果购进两种饮料的总费用不超过7000元，那么该商场如何进货才能获利最多？并求出最大利润．
| 果汁饮料 | 碳酸饮料 | |
| 进价（元/箱） | 55 | 38 |
| 售价（元/箱） | 75 | 45 |
（2）求总利润w关于x的函数关系式；
（3）如果购进两种饮料的总费用不超过7000元，那么该商场如何进货才能获利最多？并求出最大利润．
15．下列各式属于最简二次根式的是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{{a}^{2}+1}$ | C． | $\sqrt{{x}^{3}}$ | D． | $\sqrt{\frac{1}{2}}$ |
将一副三角板如图放置，使点A在DE上，BC∥DE，则∠ACE的度数为15°．
9．下列说法：①平方等于4的数只有2；②若a，b互为相反数，则$\frac{b}{a}$=-1；③若|-a|=a，则（-a）3＜0；④若ab≠0，则$\frac{a}{|a|}$+$\frac{b}{|b|}$的取值在0，1，2，-2这4个数中，不能得到的是0，其中正确的个数为（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
10．
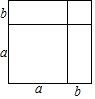如图，能根据图形中的面积说明的乘法公式是（ ）
如图，能根据图形中的面积说明的乘法公式是（ ）| A． | （a+b）（a-b）=a2-b2 | B． | （a+b）2=a2+2ab+b2 | ||
| C． | （a-b）=a2-2ab+b2 | D． | （x+p）（x+q）=x2+（p+q）x+pq |