题目内容
8.某商场欲购进果汁饮料和碳酸饮料共150箱,两种饮料每箱的进价和售价如下表所示.设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为w元(注:总利润=总售价-总进价).| 果汁饮料 | 碳酸饮料 | |
| 进价(元/箱) | 55 | 38 |
| 售价(元/箱) | 75 | 45 |
(2)求总利润w关于x的函数关系式;
(3)如果购进两种饮料的总费用不超过7000元,那么该商场如何进货才能获利最多?并求出最大利润.
分析 (1)根据商场欲购进果汁饮料和碳酸饮料共150箱,可以得到y与x的函数关系式;
(2)根据题意可以和表格中的数据可以求得总利润w关于x的函数关系式;
(3)根据(2)中关系式和题意可以列出相应的不等式,求出该商场如何进货才能获利最多,并求出最大利润.
解答 解:(1)由题意可得,
y与x的函数关系式为y=150-x,
故答案为:y=150-x;
(2)由题意可得,
w=(75-55)x+(45-38)(150-x)=13x+1050,
即总利润w关于x的函数关系式是w=13x+1050;
(3)由题意可得,
55x+38(150-x)≤7000,
解得,x≤76$\frac{8}{17}$,
∵w=13x+1050,x取正整数,
∴当x=76时,w取得最大值,此时w=2038,150-x=74,
答:如果购进两种饮料的总费用不超过7000元,那么该商场购买76箱果汁饮料,74箱碳酸饮料时能获利最多,最大利润是2038元.
点评 本题考查一次函数的应用、一元一次不等式的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质和不等式的性质解答.

练习册系列答案
相关题目
16. 如图所示,点A,O,B在同一直线上,∠COA=90°,若∠1=∠2,则图中互余的角共有( )
如图所示,点A,O,B在同一直线上,∠COA=90°,若∠1=∠2,则图中互余的角共有( )
 如图所示,点A,O,B在同一直线上,∠COA=90°,若∠1=∠2,则图中互余的角共有( )
如图所示,点A,O,B在同一直线上,∠COA=90°,若∠1=∠2,则图中互余的角共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
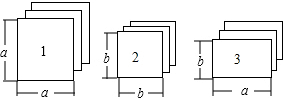 有足够多的如图所示的正方形和长方形的卡片.
有足够多的如图所示的正方形和长方形的卡片.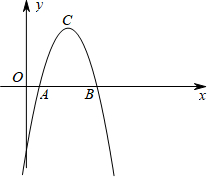 如图,已知与x轴交于点A(1,0)和B(5,0)的抛物线l的顶点为C(3,4),抛物线l′和l关于x轴对称.
如图,已知与x轴交于点A(1,0)和B(5,0)的抛物线l的顶点为C(3,4),抛物线l′和l关于x轴对称.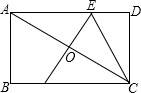 如图,在?ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则△CDE的周长为( )
如图,在?ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则△CDE的周长为( )