题目内容
12. 将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为15°.
将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为15°.
分析 根据两直线平行,内错角相等求出∠BCE=∠E=30°,然后求出∠ACE的度数.
解答 解:∵BC∥DE,
∴∠BCE=∠E=30°,
∴∠ACE=∠ACB-∠BCE=45°-30°=15°,
故答案为:15°.
点评 本题主要考查了平行线的性质,关键是掌握两直线平行,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列式子中,正确的是( )
| A. | $\sqrt{-5}$=-$\sqrt{5}$ | B. | $-\sqrt{3.6}$=-0.6 | C. | $\sqrt{(-6)^{2}}$=6 | D. | $\sqrt{36}$=±6 |
4.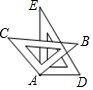 如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
 如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )| A. | ∠BAD≠∠EAC | B. | ∠DAC-∠BAE=45° | C. | ∠DAC+∠BAE=180° | D. | ∠DAC-∠BAE=90° |
1.将多项式4x2+1添加上一个单项式后能成为一个整式的完全平方,下列单项式①-4x;②?4x4;③?+4x;④-4x2;⑤-1中符合条件的是( )
| A. | ①③?? | B. | ???①②③ | C. | ??①③⑤ | D. | ???①②③④⑤ |
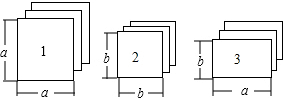 有足够多的如图所示的正方形和长方形的卡片.
有足够多的如图所示的正方形和长方形的卡片.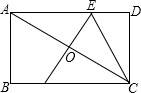 如图,在?ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则△CDE的周长为( )
如图,在?ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则△CDE的周长为( )