题目内容
1.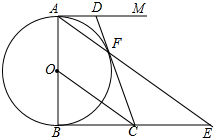 如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.
如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.(1)求证:CD是⊙O的切线.
(2)探究线段OC、CF、EF间的关系,并证明.
(3)若⊙O的半径为$\sqrt{6}$,AD=2.求EF的长.
分析 (1)连接OF,根据等腰三角形的性质得到∠OAF=∠OFA,根据平行线的性质得到∠BOC=∠OAF=∠AFO=∠FOC,推出△BOC≌△COF,于是得到∠OFC=∠OBC,得到∠OFC=∠OBC=90°,即可得到结论;
(2)连接BF,则∠AFB=∠ABE=90°,通过△ABE∽△BEF,得到BE2=AE•EF,根据三角形中位线的性质得到OC=2AE,等量代换即可得到结论;
(3)连接OD,由AM与BN是⊙0O两条切线,得到AM∥BN,求出∠DOC=90°,根据射影定理得到OF2=DF•CF,等量代换得到OF2=AD•CF,求得OF=$\sqrt{6}$,AD=2,根据勾股定理得到OD=$\sqrt{A{D}^{2}+A{O}^{2}}$=$\sqrt{10}$,OC=$\sqrt{B{C}^{2}+O{B}^{2}}$=$\sqrt{15}$,根据三角形的面积公式得到$\frac{1}{2}$AF•OD=AD•AO,即可得到结论.
解答 (1)证明:连接OF,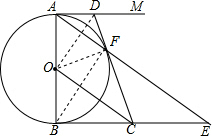 在⊙O中,
在⊙O中,
∵OF=OA,
∴∠OAF=∠OFA,
∵OC∥AE,
∴∠BOC=∠OAF=∠AFO=∠FOC,
在△BOC和△COF中,
$\left\{\begin{array}{l}{OB=OF}\\{∠BOC=∠FOC}\\{OC=OC}\end{array}\right.$
∴△BOC≌△COF,
∴∠OFC=∠OBC,
∵BN是⊙O的切线,切点为B,
∴BA⊥BN,
∴∠OFC=∠OBC=90°,
∴OF⊥CD,
∵OF是⊙O的半径,
∴DC是⊙O的切线;
(2)2CF2=EF•OC,
证明:连接BF,则∠AFB=∠ABE=90°,
∵∠BAF=∠EAB,
∴△ABE∽△BEF,
∴$\frac{BE}{EF}=\frac{AE}{BE}$,
∴BE2=AE•EF,
∵OC∥AE,AO=BO,
∴BC=CE,
∴OC=2AE,
∵BE=2CF,
∴(2CF)2=EF•2OC,
∴2CF2=EF•OC;
(3)解:连接OD,
∵AM与BN是⊙0O两条切线,
∴AM∥BN,
∴∠ADF+∠BCF=180°,
∵CD是⊙O的切线,
∴∠ODF=∠ADO,∠FCO=∠BCO,
∴∠ODF+∠OCF=90°,
∴∠DOC=90°,
∵OF⊥CD,
∴OF2=DF•CF,
∵AD=DF,
∴OF2=AD•CF,
∵OF=$\sqrt{6}$,AD=2,
∴CF=BC=CE=3,
∴OD=$\sqrt{A{D}^{2}+A{O}^{2}}$=$\sqrt{10}$,OC=$\sqrt{B{C}^{2}+O{B}^{2}}$=$\sqrt{15}$,
∴$\frac{1}{2}$AF•OD=AD•AO,
∴AF=$\frac{4\sqrt{15}}{5}$,AE=2$\sqrt{15}$,
∴EF=AE-AF=$\frac{6\sqrt{15}}{5}$.
点评 本题考查了本题主要考查了切线的性质与判定以及全等三角形的判定和性质、勾股定理,本题关键是作出辅助线.

 名校课堂系列答案
名校课堂系列答案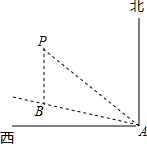 如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?
如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?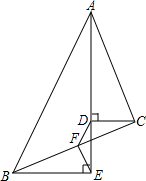 如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$.
如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$. 如图,在平面直角坐标系中,分别描出下列各点A(0,0),B(5,4),C(3,0),D(5,1),E(5,-1),F(4,-2),并按A-B-C-D-E-C-F-A顺序连接起来.
如图,在平面直角坐标系中,分别描出下列各点A(0,0),B(5,4),C(3,0),D(5,1),E(5,-1),F(4,-2),并按A-B-C-D-E-C-F-A顺序连接起来. 一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是$\sqrt{193}$.
一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是$\sqrt{193}$.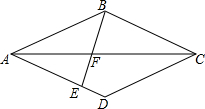 如图,菱形ABCD,过点B作直线BE,使得∠ABE=∠BCA,分别交AC、AD于点F、E.若AB=CF.则$\frac{AE}{AD}$=$\frac{\sqrt{5}-1}{2}$.
如图,菱形ABCD,过点B作直线BE,使得∠ABE=∠BCA,分别交AC、AD于点F、E.若AB=CF.则$\frac{AE}{AD}$=$\frac{\sqrt{5}-1}{2}$.