题目内容
10.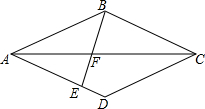 如图,菱形ABCD,过点B作直线BE,使得∠ABE=∠BCA,分别交AC、AD于点F、E.若AB=CF.则$\frac{AE}{AD}$=$\frac{\sqrt{5}-1}{2}$.
如图,菱形ABCD,过点B作直线BE,使得∠ABE=∠BCA,分别交AC、AD于点F、E.若AB=CF.则$\frac{AE}{AD}$=$\frac{\sqrt{5}-1}{2}$.
分析 设AB=CF=a,AF=b,由△ABF∽△ACB得$\frac{AB}{AC}$=$\frac{AF}{AB}$,所以a2=b(a+b),求出b、a之间的关系,再利用AE∥BC,得$\frac{AE}{BC}$=$\frac{AF}{FC}$即可解决问题.
解答 解: 设AB=CF=a,AF=b,
设AB=CF=a,AF=b,
∵∠BAF=∠BAC,∠ABF=∠ACB,
∴△ABF∽△ACB,
∴$\frac{AB}{AC}$=$\frac{AF}{AB}$,
∴a2=b(a+b),
∴b2+ba-a2=0,
∴b=$\frac{-1+\sqrt{5}}{2}$a(或b=$\frac{-1-\sqrt{5}}{2}$a舍弃),
∴$\frac{b}{a}$=$\frac{\sqrt{5}-1}{2}$,
∵四边形ABCD是菱形,
∴AE∥BC,∴AD=BC,
∴$\frac{AE}{BC}$=$\frac{AF}{FC}$=$\frac{\sqrt{5}-1}{2}$,
∴$\frac{AE}{AD}$=$\frac{\sqrt{5}-1}{2}$,
故答案为$\frac{\sqrt{5}-1}{2}$.
点评 本题考查菱形的性质、相似三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是相似三角形性质的正确应用,利用方程思想解决问题,是数形结合的好题目,所以中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.抛物线y=2(x+3)(x-1)的对称轴是( )
| A. | x=1 | B. | x=-1 | C. | x=$\frac{1}{2}$ | D. | x=-2 |
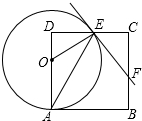 如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.
如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.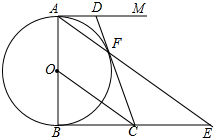 如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.
如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.