题目内容
2.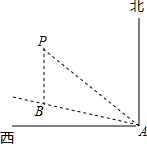 如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?
如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?
分析 延长PB交AN于G,作PH⊥AB延长线于H,根据题意知∠PAG=45°、∠PAH=30°,设PH=x,表示出AG、AB、PB的长,由△PBH∽△ABG得$\frac{PB}{AB}=\frac{PH}{AG}$,从而求出x的值比较即可.
解答 解:如图,延长PB交AN于G,作PH⊥AB延长线于H,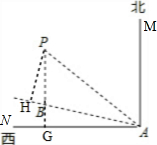
由题意知∠PAM=45°,∠BAM=75°,AM⊥AN,PB∥AM,
∴PG⊥AN,∠PAG=45°,∠GAH=15°,
∴∠PAH=30°,
∴AP=2PH,PG=AG=$\frac{\sqrt{2}}{2}$AP,
设PH=x,则AP=2x,PG=AG=$\sqrt{2}$x,
由题意知,AB=$\frac{24}{60}$×40=16,
∴BG=$\sqrt{1{6}^{2}-{x}^{2}}$,PB=PG-BG=x-$\sqrt{1{6}^{2}-{x}^{2}}$,
∵∠PHB=∠AGH=90°,∠PBH=∠ABG,
∴△PBH∽△ABG,
∴$\frac{PB}{AB}=\frac{PH}{AG}$,即$\frac{x-\sqrt{1{6}^{2}-{x}^{2}}}{16}$=$\frac{x}{\sqrt{2}x}$,
整理,得:${x}^{2}-8\sqrt{2}x-64=0$,
解得:x=4$\sqrt{2}$+4$\sqrt{6}$或x=4$\sqrt{2}$-4$\sqrt{6}$(舍),
∴PH=4$\sqrt{2}$+4$\sqrt{6}$≈15.5>9,
故船可以按原方向继续航行.
点评 本题主要考查解直角三角形的实际应用,构建直角三角形表示出各边长度是解题的前提,由相似三角形的性质求得线段的长是关键.

练习册系列答案
相关题目
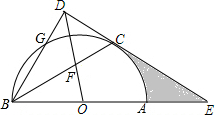 如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.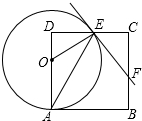 如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.
如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.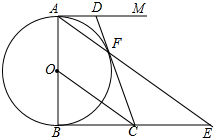 如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.
如图,AB是⊙O的直径,AM与BN是⊙0O两条切线,F是⊙O上的一点,连接AF并延长交BN于E,过点O作OC∥AE交BN于点C,连接CF并延长交AM于D.