题目内容
12.先化简,再求值.(1)2(2x2-3x-1)-3(3x2-4x+1)-4(4x2+3x-3),其中x=-2,y=-3.
(2)3x2y-[2xy2-2(xy-$\frac{3}{2}$x2y)]+3xy2,其中x=3,y=-$\frac{1}{3}$.
分析 (1)先去括号,然后合并同类项,最后代入计算即可.
(2)先去括号,然后合并同类项,最后代入计算即可.
解答 解:(1)原式=4x2-6x-2-9x2+12x-3-16x2-12x+12
=-21x2-6x+7,
当x=-2时,原式=-21×4+12+7=-65.
(2)原式=3x2y-2xy2+2xy-3x2y+3xy2
=xy2+2xy,
当x=3,y=-$\frac{1}{3}$时,原式=3×$\frac{1}{9}$-2=-$\frac{5}{3}$.
点评 本题考查整式的加减-化简求值,熟练掌握去括号法则、合并同类项法则是解题的关键,属于中考常考题型.

练习册系列答案
相关题目
7.下面的说法中,正确的是( )
| A. | 若ac=bc,则a=b | B. | 若$\frac{1}{2}$-x=1,则x=2 | C. | 若|x|=|y|,则x=y | D. | 若$\frac{x}{b}=\frac{y}{b}$,则x=y |
4. 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x+6交x轴于点A,交y轴于点B,D1是线段AB的中点,过D1作D1E1⊥x轴于E1,连接BE1交OD1于D2;过D2作D2E2⊥x轴于E2,连接BE2交OD1于D3;过D3作D3E3⊥x轴于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn为( )
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x+6交x轴于点A,交y轴于点B,D1是线段AB的中点,过D1作D1E1⊥x轴于E1,连接BE1交OD1于D2;过D2作D2E2⊥x轴于E2,连接BE2交OD1于D3;过D3作D3E3⊥x轴于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn为( )
 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x+6交x轴于点A,交y轴于点B,D1是线段AB的中点,过D1作D1E1⊥x轴于E1,连接BE1交OD1于D2;过D2作D2E2⊥x轴于E2,连接BE2交OD1于D3;过D3作D3E3⊥x轴于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn为( )
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x+6交x轴于点A,交y轴于点B,D1是线段AB的中点,过D1作D1E1⊥x轴于E1,连接BE1交OD1于D2;过D2作D2E2⊥x轴于E2,连接BE2交OD1于D3;过D3作D3E3⊥x轴于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn为( )| A. | $\frac{24}{(n+1)^{2}}$ | B. | $\frac{12}{(n+1)^{2}}$ | C. | $\frac{24}{{n}^{2}}$ | D. | $\frac{12}{{n}^{2}}$ |
 如图,在矩形ABCD中,M,N分别是AD,BC的中点,P,Q分别是BM,DN的中点
如图,在矩形ABCD中,M,N分别是AD,BC的中点,P,Q分别是BM,DN的中点
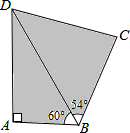 如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:
如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据: 如图,C是线段BD上一点,分别以BC和CD为边长,在直线BD的同一侧作两个等边三角形,△ABC和△ECD,连接BE和AD,BE与AC交于点F,AD与CE交于点G.
如图,C是线段BD上一点,分别以BC和CD为边长,在直线BD的同一侧作两个等边三角形,△ABC和△ECD,连接BE和AD,BE与AC交于点F,AD与CE交于点G.