Question

3．如图，在矩形ABCD中，M，N分别是AD，BC的中点，P，Q分别是BM，DN的中点
（1）求证：四边形BNDM是平行四边形．
（2）猜想：四边形MPNQ是哪种特殊的平行四边形？并证明你的猜想．

Answer 1

分析 （1）因为M，N分别是AD，BC的中点，由矩形的性质可得DM=BN，DM∥BN，利用平行四边形的判定定理可得结论；
（2）由四边形DMBN是平行四边形，求出BM=DN，BM∥DN，求出三角形MPNQ是平行四边形，根据直角三角形斜边上中线性质求出MQ=NQ，根据菱形判定推出即可．

解答 （1）证明：∵四边形ABCD是矩形，
∴AD∥BC，AD=BC，
∵M、N分别AD、BC的中点，
∴DM=BN，
∴四边形DMBN是平行四边形；

（2）解：四边形MPNQ是菱形．
∵四边形DMBN是平行四边形，
∴BM=DN，BM∥DN，
∵P、Q分别BM、DN的中点，
∴MP=NQ，MP∥NQ，
∴四边形MPNC是平行四边形，
连接MN，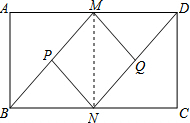
∵四边形ABCD是矩形，
∴AD∥BC，AD=BC，
∵M、N分别AD、BC的中点，
∴DM=CN，
∴四边形DMNC是矩形，
∴∠DMN=∠C=90°，
∵Q是DN中点，
∴MQ=NQ，
∴四边形MPNQ是菱形．

点评 本题考查了平行四边形的性质和判定，菱形的判定，矩形的性质，综合运用各性质定理是解答此题的关键．