题目内容
17.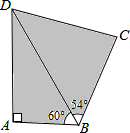 如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:
如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:∠A=90°,∠ABD=60°,∠CBD=54°,AB=200m,BC=300m.
请你计算出这片水田的面积.
(参考数据:sin54°≈0.809,cos54°≈0.588,tan54°≈1.376,$\sqrt{3}$≈1.732)
分析 作CM⊥BD于M,由含30°角的直角三角形的性质求出BD,由勾股定理求出AD,求出△ABD的面积,再由三角函数求出CM,求出△BCD的面积,然后根据S四边形ABCD=S△ABD+S△BCD列式计算即可得解.
解答 解: 作CM⊥BD于M,如图所示:
作CM⊥BD于M,如图所示:
∵∠A=90°,∠ABD=60°,
∴∠ADB=30°,
∴BD=2AB=400m,
∴AD=$\sqrt{3}$AB=200$\sqrt{3}$m,
∴△ABD的面积=$\frac{1}{2}$×200×200$\sqrt{3}$=20000$\sqrt{3}$(m2),
∵∠CMB=90°,∠CBD=54°,
∴CM=BC•sin54°=300×0.809=242.7m,
∴△BCD的面积=$\frac{1}{2}$×400×242.7=48540(m2),
∴这片水田的面积=20000$\sqrt{3}$+48540≈83180(m2).
点评 本题考查了勾股定理,由含30°角的直角三角形的性质,三角函数的运用;熟练掌握勾股定理,由三角函数求出CM是解决问题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
7.若不等式组$\left\{\begin{array}{l}{1<x<2}\\{x>k}\end{array}\right.$有解,则k的取值范围是( )
| A. | k<2 | B. | k≥2 | C. | k<1 | D. | 1≤k<2 |
5.多项式2x2-xy+y2与另一个多项式的差是3xy-x2,则这个多项式是( )
| A. | x2-2xy+y2 | B. | 2x2-4xy | C. | -2xy+y2 | D. | 3x2-4xy+y2 |
2.下列说法错误的是( )
| A. | $\frac{x+1}{7}$的常数项是1 | B. | a2+2ab+b2是二次三项式 | ||
| C. | x+$\frac{1}{x}$不是多项式 | D. | 单项式πr2h的系数是π |
 如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O
如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O
 如图,在四边形ABCD中,已知∠B=60°,∠C=2∠B,由这些条件你能判断平行的两条直线是AB∥CD.
如图,在四边形ABCD中,已知∠B=60°,∠C=2∠B,由这些条件你能判断平行的两条直线是AB∥CD.