题目内容
17.已知⊙O的半径为10,弦AB∥CD,AB=12,CD=16,则AB和CD的距离为14或2.分析 分两种情况:①当AB、CD在圆心O的两侧时,如图1,作辅助线,构建两个直角三角形,先由垂径定理得出BF和ED的长,再利用勾股定理计算出OE和OF的长,相加即可求出距离EF的长;
②当AB、CD在圆心O的同侧时,如图2,同理求得距离EF的长.
解答 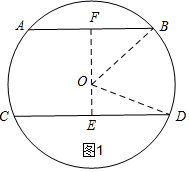 解:分两种情况:
解:分两种情况:
①当AB、CD在圆心O的两侧时,如图1,
过O作OE⊥CD于E,延长EO将AB于F,连接OD、OB,
∵AB∥CD,
∴EF⊥AB,
∴ED=$\frac{1}{2}$CD,BF=$\frac{1}{2}$AB,
∵AB=12,CD=16,
∴ED=$\frac{1}{2}$×16=8,BF=$\frac{1}{2}$×12=6,
由勾股定理得:OE=$\sqrt{O{D}^{2}-E{D}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,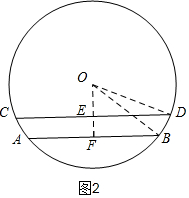
OF=$\sqrt{O{B}^{2}-B{F}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴EF=OE+OF=6+8=14;
②当AB、CD在圆心O的同侧时,如图2,
同理得:EF=OF-OE=8-6=2,
综上所述,AB和CD的距离为14或2.
点评 本题考查了垂径定理和两平行线的距离,熟练掌握垂径定理,应用了垂直弦的直径平分这条弦,恰当地作辅助线构建半径和弦心距,这是圆中常作的辅助线,要熟练掌握;本题还考查了分类讨论的思想,分别求出弦心距作和与差得出两平行线的距离.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
2.已知Rt△ABC中,a、b为直角边,c为斜边,h为斜边上的高,则下面说法错误的是( )
| A. | ab=ch | |
| B. | h<a | |
| C. | 以ah、bh、ab为边的三角形是直角三角形 | |
| D. | 以a+b、ab、c为边的三角形是直角三角形 |
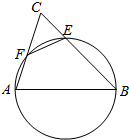 如图,以AB=6为直径的圆与△ABC的两边分别交于E,F两点,∠ACB=60°,则EF=3.
如图,以AB=6为直径的圆与△ABC的两边分别交于E,F两点,∠ACB=60°,则EF=3.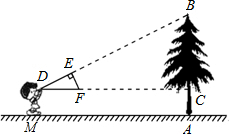 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度DM=150cm,CD=800cm,则树高AB=550cm.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度DM=150cm,CD=800cm,则树高AB=550cm.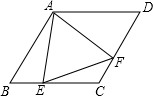 如图所示,在菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,∠BAE=24°,求∠CEF的度数.
如图所示,在菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,∠BAE=24°,求∠CEF的度数.