题目内容
9.在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,且两弦在圆心O的异侧,若AB=24,则CD的长为2$\sqrt{165}$.分析 作辅助线,构建直角三角形,由弦AB和CD的距离为7,得EF=7,根据垂径定理得:ED=$\frac{1}{2}$CD,BF=$\frac{1}{2}$AB=$\frac{1}{2}$×24=12,先利用勾股定理求OF的长,则OE=2,所以得ED的长,即得出CD的长.
解答 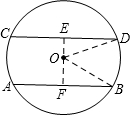 解:过O作OE⊥CD于E,延长EO交AB于F,连接OD、OB,
解:过O作OE⊥CD于E,延长EO交AB于F,连接OD、OB,
∵AB∥CD,
∴EF⊥AB,
∴ED=$\frac{1}{2}$CD,BF=$\frac{1}{2}$AB=$\frac{1}{2}$×24=12,
∵⊙O的半径为13,
∴OD=OB=13,
在Rt△OFB中,OF=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∵EF=7,
∴OE=7-5=2,
∴ED=$\sqrt{1{3}^{2}-{2}^{2}}$=$\sqrt{165}$,
∴CD=2ED=2$\sqrt{165}$.
点评 本题考查了垂径定理和两平行线的距离,作弦心距和连接半径是圆中常作的辅助线,构建直角三角形利用勾股定理求边长;本题有“两弦在圆心O的异侧“这一条件,如果没有这一条件要分两种情况进行讨论.

练习册系列答案
相关题目
4.某公司2007年的利润是a万元,计划以后每年在前一年的基础上增长m%,则2010年的利润是( )
| A. | a(1+m%)2 | B. | a(1+m%)3 | C. | a(1+m%)4 | D. | (a+m%)3 |
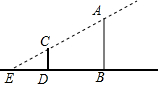 小芳的房间有高为3m的玻璃窗,她站在室内离窗户4m的地方向外看,她能看到窗前面一楼房的高度范围是18m(楼房之间的距离为20m)
小芳的房间有高为3m的玻璃窗,她站在室内离窗户4m的地方向外看,她能看到窗前面一楼房的高度范围是18m(楼房之间的距离为20m) 如图所示,在梯形ABCD中,DC∥AB,$\frac{DC}{AB}$=$\frac{1}{3}$,MN为中位线,EF∥AB且通过AC与BD的交点,点E,F分别在AD,BC上,则梯形CDEF,梯形FEMN,梯形NMAB面积的连比等于5:7:20.
如图所示,在梯形ABCD中,DC∥AB,$\frac{DC}{AB}$=$\frac{1}{3}$,MN为中位线,EF∥AB且通过AC与BD的交点,点E,F分别在AD,BC上,则梯形CDEF,梯形FEMN,梯形NMAB面积的连比等于5:7:20.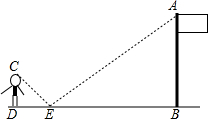 如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.
如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.