题目内容
4．
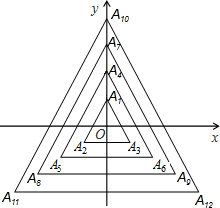如图，所有的三角形都有一个顶点位于y轴上，另外两个顶点分别位于三、四象限，且位于y轴上的点到原点的距离，与位于三、四象限内的点到两坐标轴的距离都相等，这些距离从内到外分别是1、2、3…，顶点依次用A1、A2、A3、A4…表示，则顶点A2011的坐标是（0，670）．
分析 根据三角形的特征罗列出部分顶点的坐标，分析、寻找出规律“A3n（n，-n），A3n+1（0，n），A3n+2（-n，-n）”，依此规律即可得出顶点A2011的坐标．
解答 解：观察，发现规律：A1（0，1），A2（-1，-1），A3（1，-1），A4（0，2），A5（-2，-2），A6（2，-2），…，
∴A3n（n，-n），A3n+1（0，n），A3n+2（-n，-n）．
∵2011=3×670+1，
∴顶点A2011的坐标是（0，670）．
故答案为：（0，670）．
点评 本题考查了规律型中的点的坐标，解题的关键是找出规律“A3n（n，-n），A3n+1（0，n），A3n+2（-n，-n）”．本题属于基础题，难度不大，解决该题型题目时，根据三角形的特征罗列出部分顶点A的坐标，根据坐标发现规律是关键．
练习册系列答案
相关题目
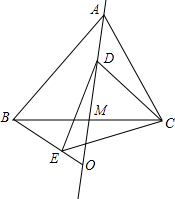如图，在等边△ABC中，线段AM为BC边上的中线，动点D在直线AM上时，以CD为一边在CD的下方作等边△CDE，设直线BE与直线AM的交点为O．
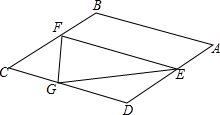如图，在菱形ABCD中，AB=$\sqrt{3}$，∠B=120°，E是AD边上的一个动点（不与点A，D重合），EF∥AB交BC于点F，点G在CD上，DG=DE．
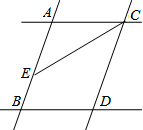如图，已知AB∥CD，AC∥BD，CE平分∠ACD．
16．方程$\frac{5}{{x}^{2}+x}$+$\frac{3}{{x}^{2}-x}$=$\frac{6}{{x}^{2}-1}$的解为（ ）
| A． | x=1 | B． | x=-1 | C． | x=$\frac{3}{5}$ | D． | 无解 |