题目内容
13．计算：$\frac{{a}^{2}}{a-3}-\frac{9}{a-3}$=a+3；（1$-\frac{1}{a+1}$）÷a$\frac{1}{a+1}$．分析 根据同分母分式的加减，分子相加减，分母不变，可得答案；
根据除以一个数等于成一这个数的倒数，可得答案．
解答 解：$\frac{{a}^{2}}{a-3}-\frac{9}{a-3}$=$\frac{{a}^{2}-9}{a-3}$=$\frac{（a+3）（a-3）}{a-3}$=a+3；
（1$-\frac{1}{a+1}$）÷a=$\frac{a+1-1}{a+1}$×$\frac{1}{a}$=$\frac{1}{a+1}$，
故答案为：a+3；$\frac{1}{a+1}$．
点评 本题考查了分式的加减，同分母分式的加减，分子相加减，分母不变；注意要化成最简分式．
练习册系列答案
相关题目
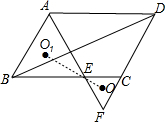如图，在?ABCD中，∠A的平分线分别与BC及DC的延长线交于点E、F，点O、O1分别为△CEF、△ABE的外心
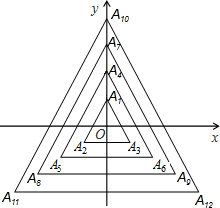如图，所有的三角形都有一个顶点位于y轴上，另外两个顶点分别位于三、四象限，且位于y轴上的点到原点的距离，与位于三、四象限内的点到两坐标轴的距离都相等，这些距离从内到外分别是1、2、3…，顶点依次用A1、A2、A3、A4…表示，则顶点A2011的坐标是（0，670）．
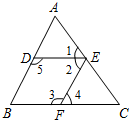推理填空：如图，根据图形填空
5．
△ABC与?DEFG如图放置，点D，G分别在边AB，AC上，E，F在BC上，已知BE=DE，CF=FG，则∠A的度数为（ ）
△ABC与?DEFG如图放置，点D，G分别在边AB，AC上，E，F在BC上，已知BE=DE，CF=FG，则∠A的度数为（ ）| A． | 80° | B． | 90° | C． | 100° | D． | 110° |
2．
如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序为（1，0）、（2，0）、（2，1）、（1，1）、（1，2）、（2，2）、…根据这个规律，第2016个点的坐标为（ ）
如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序为（1，0）、（2，0）、（2，1）、（1，1）、（1，2）、（2，2）、…根据这个规律，第2016个点的坐标为（ ）| A． | （45，13） | B． | （45，9） | C． | （45，22） | D． | （45，0） |