题目内容
14.关于x的方程x2+2x+2k-4=0有两个不相等实数根,写出一个满足条件的k的值:k=1.分析 由关于x的方程有两个不相等的实数根,得到根的判别式大于0,列出关于k的不等式,求出不等式的解集即可得到k的范围.
解答 解:∵方程x2+2x+2k-4=0有两个不相等的实数根,
∴△=b2-4ac=4-8k+16>0,
解得:k$<\frac{5}{2}$,
则k的取值范围为::k$<\frac{5}{2}$.
∴k=1.
故答案为:1(k$<\frac{5}{2}$的任意实数).
点评 此题考查了一元二次方程根的判别式,一元二次方程ax2+bx+c=0(a≠0)中,当b2-4ac>0时,方程有两个不相等的实数根;b2-4ac=0时,方程有两个相等的实数根;当b2-4ac<0时,方程无解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
5. △ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
△ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
 △ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )
△ABC与?DEFG如图放置,点D,G分别在边AB,AC上,E,F在BC上,已知BE=DE,CF=FG,则∠A的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
2. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、…根据这个规律,第2016个点的坐标为( )| A. | (45,13) | B. | (45,9) | C. | (45,22) | D. | (45,0) |
9.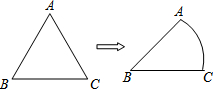 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )| A. | ($\frac{60}{π}$)° | B. | ($\frac{90}{π}$)° | C. | ($\frac{120}{π}$)° | D. | ($\frac{180}{π}$)° |
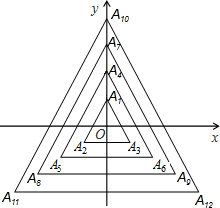 如图,所有的三角形都有一个顶点位于y轴上,另外两个顶点分别位于三、四象限,且位于y轴上的点到原点的距离,与位于三、四象限内的点到两坐标轴的距离都相等,这些距离从内到外分别是1、2、3…,顶点依次用A1、A2、A3、A4…表示,则顶点A2011的坐标是(0,670).
如图,所有的三角形都有一个顶点位于y轴上,另外两个顶点分别位于三、四象限,且位于y轴上的点到原点的距离,与位于三、四象限内的点到两坐标轴的距离都相等,这些距离从内到外分别是1、2、3…,顶点依次用A1、A2、A3、A4…表示,则顶点A2011的坐标是(0,670). 如图,⊙O的半径为5,正五边形ABCDE内接于⊙O,则$\widehat{AB}$的长度为2π.
如图,⊙O的半径为5,正五边形ABCDE内接于⊙O,则$\widehat{AB}$的长度为2π.