题目内容
10.由数字1,2,3,4,5,6,7组成一个无重复数字的七位正整数,从中任取一个,所取的数满足首位为1且任意相邻两位的数字之差的绝对值不大于2的概率等于$\frac{1}{360}$.分析 本题是一个古典概型,试验发生包含的事件是字1,2,3,4,5,6,7组成一个无重复数字的七位正整数,共有A77种结果,满足条件的事件可以在数字1234567基础上变化出符合条件的数字,分类得到结果数,得到概率.
解答 解:∵试验发生包含的事件是字1,2,3,4,5,6,7组成一个无重复数字的七位正整数,共有A77种结果,
满足条件的事件是首位为1且任意相邻两位的数字之差的绝对值不大于2,
对于数字1234567,以这个为标准,在这个数字基础上变化出符合条件的数字,
满足条件的有1234567,1234576,1234657,1234675,1235467,
1235764,1243567,1243576,1324567,1324576,1324657,
1324675,1246753,1357642共14种结果,
∴要求的概率是p=$\frac{14}{{A}_{7}^{7}}$=$\frac{1}{360}$;
故答案为$\frac{1}{360}$.
点评 本题考查古典概型及其概率公式,考查带有一定限制条件的数字的排列问题,这是一种典型的概率题目.

练习册系列答案
相关题目
2.若实数a,b满足a2+3a=2,b2+3b=2,且a≠b,则(1+a2)(1+b2)=( )
| A. | 18 | B. | 12 | C. | 9 | D. | 6 |
19.函数y=(m2-m)${x}^{{m}^{2}-3m+1}$是反比例函数,则( )
| A. | m≠0 | B. | m≠0且m≠1 | C. | m=2 | D. | m=1或2 |
 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.
如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.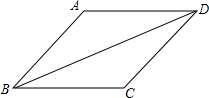 如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$.
如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$.