题目内容
5.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4.求AC和BD的长.分析 根据菱形的性质对角线互相垂直平分,在RT△AOB中利用勾股定理即可解决问题.
解答 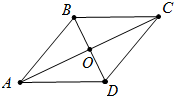 解:如图,∵四边形ABCD是菱形,
解:如图,∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC,BO=OD,
在RT△ABO中,∵∠AOB=90°,AB=5,AO=4,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AC=2AO=8,BD=2BO=6.
点评 本题考查菱形的性质、勾股定理等知识,解题的关键是菱形的性质的正确应用,记住菱形的对角线互相垂直平分,属于中考常考题型.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
15.下列函数是二次函数的是( )
| A. | y=8x2+1 | B. | y=2x-3 | C. | y=3x2+$\frac{1}{{x}^{2}}$ |
16.n个连续偶数按规律排成表:
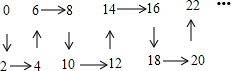
根据规律,从2016到2018,箭头的方向依次应为( )
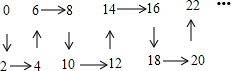
根据规律,从2016到2018,箭头的方向依次应为( )
| A. | ↑→ | B. | →↑ | C. | ↓→ | D. | →↓ |
20.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之差的绝对值为2或4的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
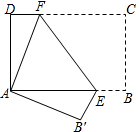 如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.
如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.