题目内容
20.已知a、b为实数,关于x的方程|x2+ax+b|=2恒有三个不等的实数根.(1)求b的最小值;
(2)若该方程的三个不等实根,恰为一个三角形三内角的度数,求证该三角形必有一个内角是60°
(3)若该方程的三个不等实根恰为一直角三角形的三条边,求a和b的值.
分析 (1)由绝对值的意义,原方程可以化为两个方程,又因为原方程有三个根,所以这两个方程中有一个方程是有不等实数根,有一个方程有两相等实数根,用一元二次方程根的判别式确定答案;
(2)根据三角形三内角和为180°,以及一元二次方程根与系数的关系,利用两根之和求出a的值,然后确定三角形的内角;
(3)根据根与系数的关系,利用勾股定理进行计算,求出a,b的值.
解答 解:(1)由原方程得:x2+ax+b-2=0①,x2+ax+b+2=0②,
两方程的判别式分别为:△1=a2-4b+8,△2=a2-4b-8,
∵原方程有三个根,
∴方程①,②中有一个方程有两个不等实数根,另一个方程有两个相等实数根,
即△1,△2中必有一个大于0,一个等于0,比较△1,△2,显然△1>△2,
∴△1>0,△2=0,
即$\left\{\begin{array}{l}{a^2}-4b-8=0\\{a^2}-4b+8>0\end{array}\right.$,得$\left\{\begin{array}{l}b=\frac{1}{4}{a^2}-2\\ b<\frac{1}{4}{a^2}+2\end{array}\right.$,
由$\frac{1}{4}{a^2}-2<\frac{1}{4}{a^2}+2$,可知a取任意实数
∴当 a=0 时,b的最小值是-2;
(2)由(1),设x2+ax+b=2的根为x1,x2,x2+ax+b=-2的根为x3
∴x1+x2=-a,${x_3}=-\frac{a}{2}$
由已知x1+x2+x3=180°,即$-a-\frac{a}{2}={180°}$,得a=-120
∴x3=60°即该三角形必有一个内角是60°
(3)由${△_2}={a^2}-4b-8$=0,知a2-4b=8,得${△_1}={a^2}-4b+8=16$
所以x2+ax+b=2的根为${x_{1,2}}=\frac{-a±4}{2}$,
∵$\frac{-a+4}{2}>\frac{-a}{2}>\frac{-a-4}{2}$
∴${({\frac{-a+4}{2}})^2}={({\frac{-a}{2}})^2}+{({\frac{{-a-{4^{\;}}}}{2}})^2}$,得a=-16,或a=0
当a=0时,${x_3}=-\frac{a}{2}=0$,不可能.
∴a=-16,$b=\frac{{{a^2}-8}}{4}=62$.
点评 本题考查的是一元二次方程根与系数的关系,(1)题根据方程的根的情况,用一元二次方程根的判别式进行求解.(2)题根据一元二次方程根与系数的关系以及三角形三内角和是180°进行证明.(3)题根据一元二次方程根与系数的关系以及勾股定理,并用(1)题中的结论进行计算求出a,b的值.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案| A. | y=8x2+1 | B. | y=2x-3 | C. | y=3x2+$\frac{1}{{x}^{2}}$ |
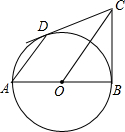 如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.
如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.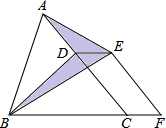 如图,已知△ABC的面积为36,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为36,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )