题目内容
12.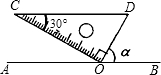 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
分析 由斜边CD∥AB,可求得∠AOC的度数,又由∠COD=90°,即可求得∠α的度数,继而求得答案.
解答 解:∵斜边CD∥AB,∠C=30°,
∴∠AOC=∠C=30°,
∵∠COD=90°,
∴∠α=180°-∠AOC-∠COD=60°,
∴sinα=sin60°=$\frac{\sqrt{3}}{2}$.
故选C.
点评 此题考查了平行线的性质以及特殊角的三角函数值.注意求得∠α的度数是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.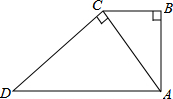 如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
△ABC与△DCA的面积比为( )
 如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则△ABC与△DCA的面积比为( )
| A. | 2:3 | B. | 2:5 | C. | 4:9 | D. | $\sqrt{2}$:$\sqrt{3}$ |
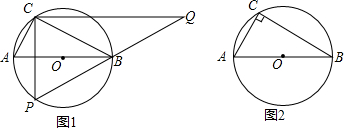 如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.
如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.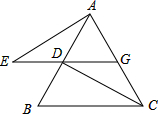 已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD.
已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD. 如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( ) 已知抛物线y=ax2+bx+c的部分图象如图所示,若y<0,则x的取值范围是-1<x<3.
已知抛物线y=ax2+bx+c的部分图象如图所示,若y<0,则x的取值范围是-1<x<3.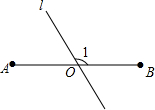 如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.
如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.